Question

10．四边形ABCD为平行四边形，AE⊥BC，垂足为点E，若AB=5，AC=2$\sqrt{5}$，AE=4，则?ABCD的周长为20或12．

Answer 1

分析 分两种情况：①根据平行四边形的性质AB=CD，AD=BC，由勾股定理求出BE和CE，得出BC，即可得出结果；②同①得：BC=BE-CE=1，得出?ABCD的周长=2（AB+BC）=12，即可得出结论．

解答 解：分两种情况：
①如图所示：
∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，
∵AE⊥BC，
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3，CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=2，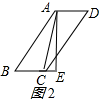
∴BC=BE+CE=5，
∴?ABCD的周长=2（AB+BC）=2×10=20；
②如图2所示：
同①得：BC=BE-CE=1，
∴?ABCD的周长=2（AB+BC）=2×6=12；
综上所述：?ABCD的周长为20或12；
故答案为：20或12．

点评 此题主要考查了平行四边形的性质、勾股定理；熟练掌握平行四边形的性质，由勾股定理求出BE和CE是解决问题的关键，注意分类讨论．