题目内容
5. 如图所示,已知等腰△ABC的底边BC与轴重合,BC=4,点B(3,0),AC交轴于点D(0,3).
如图所示,已知等腰△ABC的底边BC与轴重合,BC=4,点B(3,0),AC交轴于点D(0,3).(1)求直线AC的解析式;
(2)若点M为等腰△ABC的对称轴上一点,是否存在这样的M,使得线段DM+CM的值最小?若存在,直接写出点M的坐标;若不存在,请说明理由.
(3)连接BD,在直线AC上是否存在一点P,使S△PBD=$\frac{1}{2}$S△PBC?若存在,试求出点P的坐标;若不存在,请说明理由.
分析 (1)利用待定系数法求直线AC的解析式;
(2)作出等腰三角形的对称轴AF,因为C和B是对称点,所以BD与AF的交点就是所求的点M,利用线段垂直平分线的性质可知:直线AF:x=1,点M就是AF与BD的交点,利用方程组求解;
(3)存在,分两种情况:①点P在CD的延长线上时,点P与点A重合,则这时P(1,6);②点P在线段CD上时,利用平行线分线段成比例定理列比例式求出点P的坐标.
解答  解:(1)由题意得:C(-1,0),
解:(1)由题意得:C(-1,0),
设直线AC的解析式为:y=kx+b,
把C(-1,0)、D(0,3)代入得:$\left\{\begin{array}{l}{-k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$,
∴直线AC的解析式为:y=3x+3;
(2)存在,如图1,作对称轴交BD于M,交x轴于F,连接CM,
点C与点B关于直线AF对称,
这时CM+DM的值最小,
∵AF是BC的垂直平分线,
∴直线AF的解析式为:x=1,
设直线BD的解析式为:y=kx+b,
把B(3,0),D(0,3)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
则直线BD的解析式为:y=-x+3,
当x=1时,y=2,
∴M(1,2);
(3)①点P在CD的延长线上时,如图2,当PD=CD时,S△PBD=$\frac{1}{2}$S△PBC,
∵C(-1,0),D(0,3)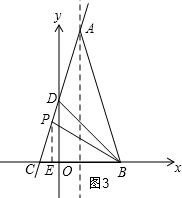
∴P(1,6)
这时点P与点A重合;
②点P在线段CD上时,如图3,当PD=$\frac{1}{2}$PC时,S△PBD=$\frac{1}{2}$S△PBC,
过P作PE⊥BC于E,则PE∥OD,
∴$\frac{PE}{OD}=\frac{CP}{CD}=\frac{CE}{CO}$,
∴$\frac{PE}{3}=\frac{2}{3}=\frac{CE}{1}$,
∴PE=2,CE=$\frac{2}{3}$,
∴P(-$\frac{1}{3}$,2),
综上所述,存在这样的P点,坐标为(1,6)或((-$\frac{1}{3}$,2).
点评 本题是一次函数的综合题,考查了利用待定系数法求一次函数的解析式,并利用方程组的解求两直线的交点坐标;本题还利用对称性求线段和的最小值,这里综合考查了三角形的三边关系及线段垂直平分线的性质;另外,本题还运用了分类讨论的思想,将三角形的面积与平行线分线段成比例定理及坐标相结合,综合性较强.

| A. | x0=x1 | B. | x0=x3 | C. | x0=x2,x0≠x4 | D. | x0=x2=x4 |
| A. | $\frac{3000}{x+50}$=$\frac{3000}{x}$×$\frac{3}{4}$ | B. | $\frac{3000}{x+50}$=$\frac{3000}{x}$÷$\frac{3}{4}$ | ||
| C. | $\frac{3000}{x+50}$=$\frac{3000}{x}$+$\frac{3}{4}$ | D. | $\frac{3000}{x+50}$=$\frac{3000}{x}$-$\frac{3}{4}$ |
| A. | (2,-5) | B. | (2,5) | C. | (5,2) | D. | (-5,2) |
| A. | 2.5×106 | B. | 0.25×10-5 | C. | 2.5×10-6 | D. | 25×10-7 |
 如图,?ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为2或2$\sqrt{3}$或$\sqrt{19}$.
如图,?ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为2或2$\sqrt{3}$或$\sqrt{19}$. 如图,正方形ABCD的边长为1,E是AD边上一动点,AE=m,将△ABE沿BE折叠后得到△GBE.延长BG交直线CD于点F.
如图,正方形ABCD的边长为1,E是AD边上一动点,AE=m,将△ABE沿BE折叠后得到△GBE.延长BG交直线CD于点F.