题目内容
2.已知一次函数y1=-ax+3(a为常数)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象在第三相交于点A(a,$\frac{a}{2}$),则y2的解析式是( )| A. | ${y_2}=\frac{9}{8x}$ | B. | ${y_2}=\frac{1}{2x}$ | C. | ${y_2}=\frac{2}{x}$ | D. | ${y_2}=-\frac{2}{x}$ |
分析 把A的坐标代入两个函数的解析式,解方程组求得k的值,从而确定函数解析式.
解答 解:根据题意得:$\left\{\begin{array}{l}{-a+3=\frac{a}{2}…①}\\{\frac{k}{a}=\frac{a}{2}…②}\end{array}\right.$,
解①得a=2,
把a=2代入②得k=2,
则y2的解析式是y2=$\frac{2}{x}$.
故选C.
点评 本题考查了反比例函数与一次函数的交点问题,理解函数图象上的点的坐标满足函数解析式,正确解方程组是关键.

练习册系列答案
相关题目
12. 如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
 如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )| A. | a | B. | 2a | C. | $\frac{3}{2}$a | D. | $\frac{5}{2}$a |
13.若点A(-5,y1),B(1,y2),C(2,y3)在反比例函数y=$\frac{-{a}^{2}-1}{x}$(a为常数)的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
10.要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
| A. | 方差 | B. | 平均数 | C. | 中位数 | D. | 众数 |
7.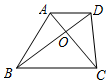 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果AO:AC=2:5,那么S△AOD:S△BOC为( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果AO:AC=2:5,那么S△AOD:S△BOC为( )
 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果AO:AC=2:5,那么S△AOD:S△BOC为( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果AO:AC=2:5,那么S△AOD:S△BOC为( )| A. | 4:25 | B. | 4:9 | C. | 2:5 | D. | 2:3 |
14.我国自主研制的世界首颗空间量子科学实验卫星“墨子号”,圆满完成4个月的在轨测试任务后,于2017年1月18日正式交付用户单位使用.在试验期间的某周,“墨子号”向地面接收站发送的信息量如下表:
这七天发送的信息量的众数是( )
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 信息量(MB) | 202 | 210 | 200 | 202 | 200 | 198 | 202 |
| A. | 198 | B. | 200 | C. | 202 | D. | 210 |
11.函数y=$\frac{1}{\sqrt{4-x}}$中自变量x的取值范围是( )
| A. | x<4 | B. | x≠4 | C. | x>4 | D. | x≤4 |
12.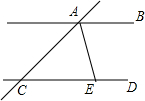 如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
 如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )| A. | 40° | B. | 110° | C. | 70° | D. | 140° |
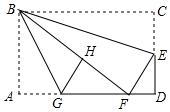 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG=$\frac{3}{2}$S△FGH.其中正确的是( )
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG=$\frac{3}{2}$S△FGH.其中正确的是( )