由此可以估计事件M发生的概率为( )

A.B.C.D.

（1）S数列的任意一项是否可以写成其某两项的差？请说明理由．

（2）①是否存在等差数列为S数列，若存在，请举例说明；若不存在，请说明理由．

②是否存在正项递增等比数列为S数列，若存在，请举例说明；若不存在，请说明理由．

【题目】下表是年我国就业人口及劳动年龄人口（劳动年龄人口包含就业人口）统计表：

则由表可知（ ）

A.年我国就业人口逐年减少

B.年我国劳动年龄人口逐年增加

C.年这年我国就业人口数量的中位数为

D.年我国劳动年龄人口中就业人口所占比重逐年增加

【题目】已知函数.

（1）若函数的图象在点处的切线方程为，求实数a，b的值；

（2）若，求的单调减区间；

（3）对一切实数，求的极小值函数，并求出的最大值.

【题目】已知函数，（x＞0）．

（1）当0＜a＜b，且f（a）＝f（b）时，求证：ab＞1；

（2）是否存在实数a，b（a＜b），使得函数y＝f（x）的定义域、值域都是[a，b]，若存在，则求出a，b的值，若不存在，请说明理由．

（3）若存在实数a，b（a＜b），使得函数y＝f（x）的定义域为[a，b]时，值域为[ma，mb]（m≠0），求m的取值范围．

【题目】若方程有两个不同的实数解，则b的取值范围是_____

（1）根据1至5月份的数据，求出y关于x的回归直线方程；

（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元，则认为所得到的回归直线方程是理想的，试问所得回归直线方程是否理想？

（3）预计在今后的销售中，销售量与单价仍然服从（1）中的关系，且该产品的成本是2.5元/件，为获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）.

参考公式：回归方程，其中.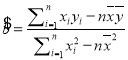

参考数据：，.

【题目】已知椭圆的上、下、左、右四个顶点分别为x轴正半轴上的某点满足.

(1)求椭圆的方程;

(2)设该椭圆的左、右焦点分别为,点在圆上,且在第一象限,过作圆的切线交椭圆于,求证:△的周长是定值．

【题目】已知函数.

（1）求证：当时，；

（2）若对任意存在和使成立，求实数的最小值.

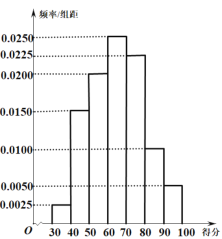
【题目】为了解广大学生家长对校园食品安全的认识，某市食品安全检测部门对该市家长进行了一次校园食品安全网络知识问卷调查，每一位学生家长仅有一次参加机会，现对有效问卷进行整理，并随机抽取出了200份答卷，统计这些答卷的得分（满分：100分）制出的频率分布直方图如图所示，由频率分布直方图可以认为，此次问卷调查的得分服从正态分布，其中近似为这200人得分的平均值（同一组数据用该组区间的中点值作为代表）.

（1）请利用正态分布的知识求；

（2）该市食品安全检测部门为此次参加问卷调查的学生家长制定如下奖励方案：

①得分不低于的可以获赠2次随机话费，得分低于的可以获赠1次随机话费：

②每次获赠的随机话费和对应的概率为：

市食品安全检测部门预计参加此次活动的家长约5000人，请依据以上数据估计此次活动可能赠送出多少话费？

附：①；②若；则，，.