题目内容
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
【答案】(1)S数列的任意一项都可以写成其某两项的差;证明见详解(2)①存在a1=kd,k∈Z,k≥﹣1满足题意;②不存在,证明见详解.
【解析】
(1)根据对新数列的定义,利用![]() 进行计算证明;
进行计算证明;
(2)①假设存在等差数列,根据数列的公差进行分类讨论即可;
②用反证法证明,假设存在满足题意的数列,结合数列![]() 的单调性,推出矛盾.
的单调性,推出矛盾.
(1)∵数列{an}是S数列,
∴对任意正整数n,总存在正整数m,使得Sn=am,
∴n≥2时,![]() ,
,
∴Sn﹣Sn﹣1=am﹣ap,即an=am﹣ap,
而n=1时,S2=aq,则a1=aq﹣a2,
故S数列的任意一项都可以写成其某两项的差;
(2)①假设存在等差数列为S数列,设其首项为a1,公差为d,
(i)当d=0时,若a1≠0,则对任意的正整数n,不
可能存在正整数m,使得Sn=am,即na1=a1;
(ii)当d=0且a1=0时,显然满足题意;
(iii)当d≠0时,由Sn=am得,
![]() ,
,
故 ,
,
∵![]() ,n=1时显然存在m=1满足上式,
,n=1时显然存在m=1满足上式,
n=2时,![]() ,
,
∴![]() ,
,
此时![]() 符合题意,
符合题意,
综上,存在a1=kd,k∈Z,k≥﹣1满足题意;
②假设存在正项递增等比数列为S数列,则a1>0,q>0,
∴对任意正整数n,总存在正整数m,使得Sn=am,
∵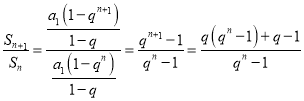
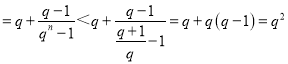 ,
,
∴![]() ,即
,即![]() ,
,
即am+1<Sn+1<am+2,
∵Sn+1∈{an}且{an}单调递增,
显然当n>logq(q+1)﹣1时,不存在t∈N,使得Sn+1=at,
这与S数列的定义矛盾.
故不存在正项递增等比数列为S数列.

 金博士一点全通系列答案
金博士一点全通系列答案【题目】对某产品1至6月份销售量及其价格进行调查,其售价x和销售量y之间的一组数据如下表所示:
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
(3)预计在今后的销售中,销售量与单价仍然服从(1)中的关系,且该产品的成本是2.5元/件,为获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本).
参考公式:回归方程![]() ,其中
,其中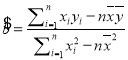 .
.
参考数据:![]() ,
,![]() .
.