2009年4月5日，北京召开“继续实行交通管理措施”新闻发布会，市交通委新闻发言人王兆荣表示，为巩固北京奥运会交通和空气质量治理成果，在广泛民意调查基础上，本市决定继续在2009年4月10日后实施按车牌尾号每周一日高峰时段停驶的交通管理措施。请你完成下面三项任务。

7．某市专家在调查研究的基础上，收集了以下关于学生健康状况的内容，请你用简洁的语言概括这两则信息的主要内容。(2分)

[材料一]

	人数	学生健康状况
出现呼吸道症状的人数	血铅含量 (几何均值)
某城市第一小学	139人	约占44%	0.298μmol/L
某城市第二小学	170人	约占21%	0.252μmol/L.

[材料二]

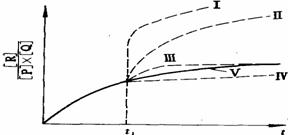
专家介绍，汽车尾气污染物中一氧化碳是有害排放物中浓度最高的，主要集中在离地面1.5米左右的高度，直接损伤人的呼吸系统。而且，一氧化碳进入人的血液后，会削弱血液向各组织输送氧的功能，危害中枢神经系统，造成理解和记忆力等障碍。此外，尾气排放的铅由于重而下沉，刚好落在儿童的呼吸带高度。

答：　　　　

5．默写(5分)　

(1)夕阳西下， 　　　。(马致远 《天净沙　 秋思》)(1分)

(2)　　 ，病树前头万木春。(刘禹锡 《酬乐天扬州初逢席上见赠》)(1分)

(3)一鼓作气，再而衰，三而竭。　　　 ，故克之。(《曹刿论战》)(1分)

(4)辛弃疾在《破阵子　 为陈同甫赋壮词以寄之》中，表明自己醉里梦里不忘仗剑出征的最终目的的诗句是：　　　 ，　　 。(2分)

4．下列作家均为同一朝代的是

①杜甫　 ②陶渊明　 ③吴敬梓　 ④柳宗元　 ⑤白居易　 ⑥辛弃疾

A．①②④　　　 B．①④⑤　　　 C．②③⑥　　　 D．③④⑤

3．对下列句子中加点词语使用有误的一项是

A．航天员从太空回来后深刻体验到一己的微不足道，他们觉得应该尽心尽意做自己喜欢的有价值有意义的事情。

　B．在徐悲鸿纪念馆中，徐悲鸿先生的大理石雕像矗立在楼前，他面容和蔼，以艺术家特有的气质微笑着迎接每一位来者。

C．当人的精神空间足够大时，挫折的冲击就变小了，这就是吃一堑，长一智。就像一块石头可以打翻一杯水，却只能在大海中溅起一点水花一样。

D．梅兰芳之所以能取得如此辉煌的成就，这和他曲不离口，拳不离手的勤学苦练、虚心求教、集百家之长于一身是分不开的。

2．下列句子中有错别字的一项是

A．她在博物馆中看到了美丽的蝴蝶标本。

B．大熊猫是珍奇的动物，象征吉祥友谊。

C．在百花山顶看百花，令人心旷神怡。

D．兽首铜像造形生动做工精细栩栩如生。

1．下列词语中加点字的读音完全正确的一项是

A.伶仃(tīnɡ)　　　　　 僻静(pì)　　　　 不耻下问(chǐ)　

B.惬意(qiè)　　　　　 霎时(chà)　　　　 言简意赅(ɡāi)

C.自诩(xǔ)　　　　　　 琐屑(xiè)　　　　 人声鼎沸(dǐnɡ)

D.修葺(qì)　　　　　　 游弋(yè)　　　　 万籁俱寂(lài)

2．6 生物作图及曲线分析

　　 生物作图在近些年的高考试题中经常出现，对能力要求比较高，要求学生会从数形中提炼出有用的信息。教师在平时的教学中，可以结合生物学知识解决一些难以理解的、比较抽象的图形和曲线。

例6：有一种酶催化反应P+Q→R，右图中的实线表示没有酶时此反应的进程。在t₁时，将催化此反应的酶加入反应混合物中。右图中的哪条线能表示此反应的真实进程(图中[P]、[Q]和[R]分别代表化合物P、Q和R的浓度)？(　　 )

　 A、Ⅰ　　 B、Ⅱ　　 C、Ⅲ　　 D、Ⅳ　　 E、Ⅴ

解析：A、B和D都不对。酶作为催化剂不能改变化学反应的平衡点即平衡常数(Keq＝[R] /[P][Q])，只能缩短达到平衡的时间。图中实线平行于横坐标的线段延长相交于纵坐标的那个交点即为此反应的Keq。Ⅰ，Ⅱ和Ⅳ三条线显然都改变了此平衡点。C正确：线Ⅲ反映了加酶后缩短了达到平衡点的时间而不改变原反应的平衡点。E不对：曲线Ⅴ从t₁至平衡前的线段不符合加酶后的真实进程。

3　 生物教学中数学建模的意义

　　 高中生物学科中涉及到的数学建模远不及这些，限于篇辐，本文在此只作简要的归纳。我们知道，实际问题是复杂多变的，数学建模需要学生具有一定的探索性和创造性。在教学过程中，充分的运用它能很好的解决一些生物学实际问题，使学生对生物学产生更大的兴趣。生命科学作为一门自然科学，其理论的深入研究必定会涉及到很多数学的问题。在生物学教学中，构建数学模型正是联系数学与生命科学的桥梁。如何将生物学理论知识转化为数学模型，这是对学生创造性地解决问题的能力的检验，也是理科教育的重要任务。

2. 5 生态系统的数学模型

　　 生态学的一般规律中，常常求助于数学模型的研究，理论生态学中涉及到大量的数学模型构建的问题。在高中生物学中有种群的动态模型研究，如：“J”与“S”型曲线；另外，种间竞争及捕食的数学模型等等。

例5：在实验室中进行了两类细菌竞争食物的实验。在两类细菌的混合培养液中测定了第Ⅰ类细菌后一代(即Z_t+1)所占总数的百分数与前一代(即Z_t)所占百分数之间的关系。在下图中，实线表示观测到的Z_t+1和Z_t之间的关系，虚线表示Z_t+1＝Z_t时的情况。从长远看，第Ⅰ类和第Ⅱ类细菌将会发生什么情况？(　　 )

A、第Ⅰ类细菌与第Ⅱ类细菌共存

B、两类细菌共同增长

C、第Ⅰ类细菌把第Ⅱ类细菌从混合培养液中排除掉

D、第Ⅱ类细菌把第Ⅰ类细菌从混合培养液中排除掉

解析：两类细菌在实验条件下，同一环境中不存在其他生物因素的作用时，竞争的结果是一种生物生存下来，另一种被淘汰现象。从上述图形的对角线(虚线)上可以看出在虚线上任取一点作横坐标与纵坐标得到的是相同的数据，这说明了同种细菌后一代与前一代在混合培养液中的比例没有变化，说明它们之间是共存的，不是竞争关系。而实线位于虚线下方，用同样的方法不难得出，第Ⅰ类细菌的后一代含量比前一代含量减少了，在竞争中是劣势的种群。本题答案为D。

2. 4 概率的计算

　 　高中生物的遗传机率的计算是教学的难点，教师通过对具体实例的解析，协助学生构建概率相加与相乘原理。比如：分类用概率相加原理；分步用概率相乘原理。

例4：A a B b×A a B B相交子代中基因型a a B B所占比例的计算。

解析：因为A a×A a相交子代中a a基因型个体占1/4，B b×B B相交子代中B B基因型个体占1/2，所以a a B B基因型个体占所有子代的1/4×1/2＝1/8。[由概率分步相乘原理，可知子代个别基因型所占比例等于该个别基因型中各对基因型出现概率的乘积]。