0 53567 53575 53581 53585 53591 53593 53597 53603 53605 53611 53617 53621 53623 53627 53633 53635 53641 53645 53647 53651 53653 53657 53659 53661 53662 53663 53665 53666 53667 53669 53671 53675 53677 53681 53683 53687 53693 53695 53701 53705 53707 53711 53717 53723 53725 53731 53735 53737 53743 53747 53753 53761 447348
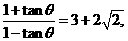 则
则 的值为( )
的值为( )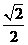 B.
B.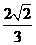 C.
C.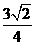 D.
D.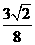
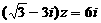 (i是虚数单位),则z=
( )
(i是虚数单位),则z=
( )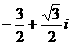 B.
B. 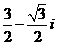 C.
C.
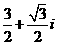 D.
D.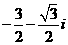
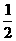 B.
B. 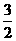 C.
C. 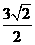 D.
D. 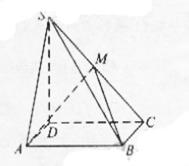 (2009全国卷Ⅰ理)(本小题满分12分)(注意:在试题卷上作答无效)
(2009全国卷Ⅰ理)(本小题满分12分)(注意:在试题卷上作答无效)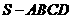 中,底面
中,底面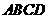 为矩形,
为矩形,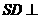 底面
底面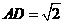
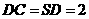 ,点M在侧棱
,点M在侧棱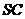 上,
上,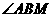 =60°
=60°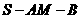 的大小。
的大小。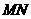 ∥
∥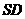 交
交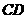 于N,作
于N,作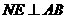 交
交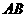 于E,
于E,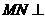 面
面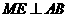 ,
,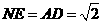
 设
设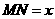 ,则
,则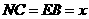 ,
, 中,
中,
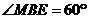
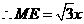 。
。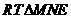 中由
中由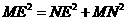
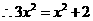
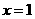 ,从而
,从而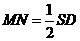
 M为侧棱
M为侧棱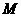 作
作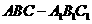 中,
中,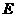 、
、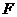 分别是
分别是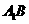 、
、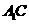 的中点,点
的中点,点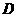 在
在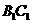 上,
上,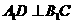 。
。 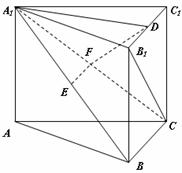 求证:(1)EF∥平面ABC;
求证:(1)EF∥平面ABC; 
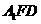
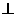 平面
平面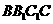 .
.

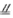
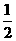
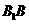 ,从而EF
,从而EF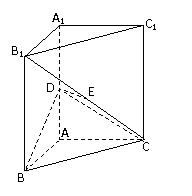

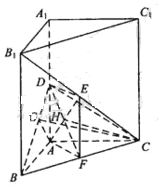
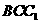 ,故AF⊥平面
,故AF⊥平面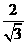 。又AB=2,BC=
。又AB=2,BC=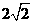 ,故AF=
,故AF=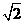 。
。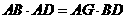 得2AD=
得2AD=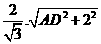 ,解得AD=
,解得AD=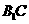 与平面BCD所成的角。.
与平面BCD所成的角。. 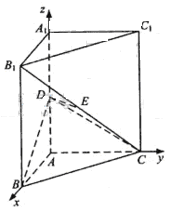 因ADEF为正方形,AD=
因ADEF为正方形,AD=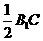 =2,
=2,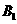 (1,0,2c),E(
(1,0,2c),E(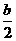 ,c).
,c).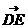 =(
=(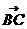 =(-1,b,0).由DE⊥平面
=(-1,b,0).由DE⊥平面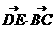 =0,求得b=1,所以 AB=AC。
=0,求得b=1,所以 AB=AC。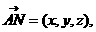 则
则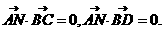
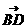 =(-1,0,c),故
=(-1,0,c),故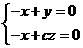
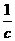 ,
,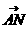 =(1,1,
=(1,1,  的法向量
的法向量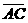 =(0,1,0)
=(0,1,0)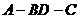 为60°知,
为60°知,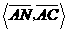 =60°,
=60°,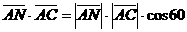 °,求得
°,求得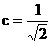
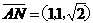 ,
, 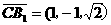
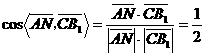 ,
,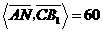 °
°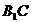 与平面
与平面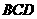 所成的角为30°
所成的角为30°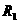 ,
,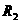 ,
,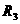 满足
满足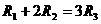 ,则它们的表面积
,则它们的表面积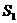 ,
,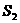 ,
,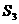 ,满足的等量关系是___________.
,满足的等量关系是___________. 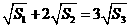
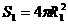 ,
,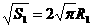 ,同理:
,同理: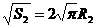
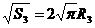 ,即R1=
,即R1=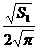 ,R2=
,R2=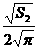 ,R3=
,R3=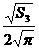 ,由
,由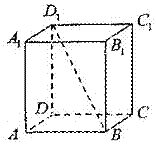 (2009年上海卷理)如图,若正四棱柱
(2009年上海卷理)如图,若正四棱柱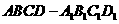 的底面连长为2,高 为4,则异面直线
的底面连长为2,高 为4,则异面直线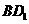 与AD所成角的大小是______________(结果用反三角函数表示).
与AD所成角的大小是______________(结果用反三角函数表示).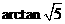
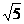 ,tan∠A1D1B=
,tan∠A1D1B=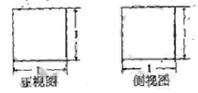
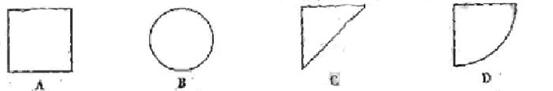
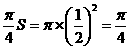 ,高为1,则体积是
,高为1,则体积是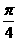 ;当俯视是C时,该几何是直三棱柱,故体积是
;当俯视是C时,该几何是直三棱柱,故体积是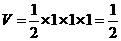 ,当俯视图是D时,该几何是圆柱切割而成,其体积是
,当俯视图是D时,该几何是圆柱切割而成,其体积是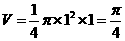 .故选C.
.故选C.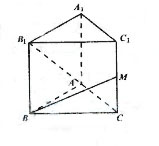 (2009四川卷理)如图,已知正三棱柱
(2009四川卷理)如图,已知正三棱柱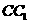 的中点,则异面直线
的中点,则异面直线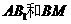 所成的角的大小是
。
所成的角的大小是
。 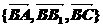 ,则
,则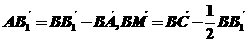
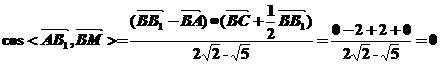 ,故填写
,故填写 。
。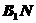 ,则
,则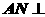 面
面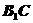 ,∴
,∴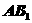 在面
在面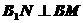 ,由三垂线定理得
,由三垂线定理得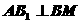 ,故填写
,故填写