0 53586 53594 53600 53604 53610 53612 53616 53622 53624 53630 53636 53640 53642 53646 53652 53654 53660 53664 53666 53670 53672 53676 53678 53680 53681 53682 53684 53685 53686 53688 53690 53694 53696 53700 53702 53706 53712 53714 53720 53724 53726 53730 53736 53742 53744 53750 53754 53756 53762 53766 53772 53780 447348

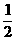 (9+10)=9.5(米)。
(9+10)=9.5(米)。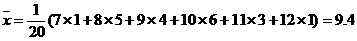 (米)
(米)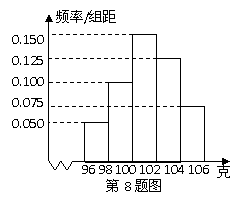
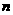 ,
,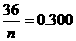 ,所以
,所以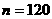 ,净重大于或等于98克并且小于
,净重大于或等于98克并且小于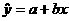 。其中
。其中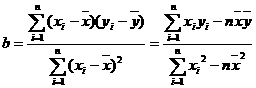 ,
,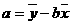 。我们称这个方程为y对x的回归直线方程。
。我们称这个方程为y对x的回归直线方程。 =频率。
=频率。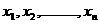 ,那么
,那么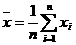 叫做这n个数据平均数;
叫做这n个数据平均数;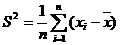 叫做这n个数据方差;同时
叫做这n个数据方差;同时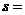
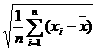 叫做这n个数据的标准差。
叫做这n个数据的标准差。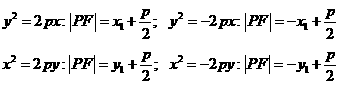
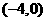 、
、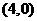 ,椭圆上一点
,椭圆上一点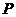 到两焦点距离的和等于
到两焦点距离的和等于 ;
;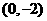 、
、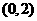 ,并且椭圆经过点
,并且椭圆经过点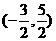 ;
;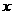 轴上,
轴上,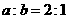 ,
,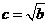 ;
;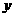 轴上,
轴上,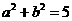 ,且过点
,且过点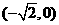 ;
;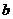 ,
,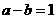 ;
;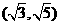 。
。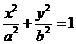 (
(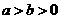 ),
),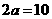 ,
,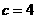 ,∴
,∴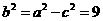 ,
,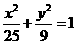 。
。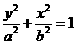 (
(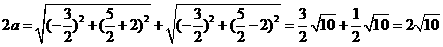 ,
,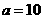 ,又∵
,又∵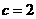 ,∴
,∴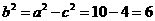 ,
,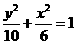 。
。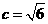 ,∴
,∴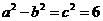 ,①
,①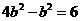 ,
,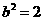 ,∴
,∴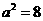 ,又∵焦点在
,又∵焦点在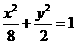 。
。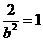 ,∴
,∴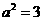 ,
,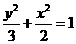 .
. ,∴
,∴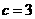 ,
,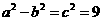 ,又∵
,又∵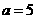 ,
,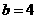 ,
,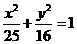 或
或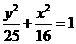 .
.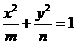 (
(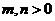 ),
),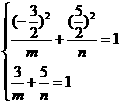 得
得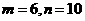 ,
,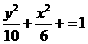 .
.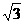 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。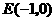 ,它的一个焦点为
,它的一个焦点为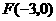 ,相应于焦点
,相应于焦点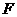 的准线方程为
的准线方程为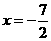 ,则这个椭圆的方程是( )
,则这个椭圆的方程是( )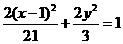 B.
B.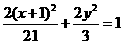
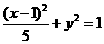 D.
D.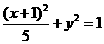
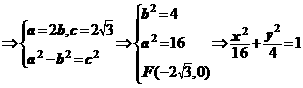 为所求;
为所求;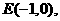 它的一个焦点为
它的一个焦点为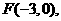
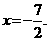
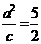 ,
,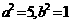 ,则这个椭圆的方程是
,则这个椭圆的方程是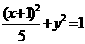 ,选D。
,选D。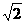 ,焦点到相应准线的距离为1,则该椭圆的离心率为( )
,焦点到相应准线的距离为1,则该椭圆的离心率为( )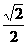 (C)
(C) 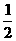 (D)
(D)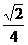
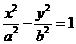 (a>0,b>0)的渐近线与抛物线y=x2 +1相切,则该双曲线的离心率等于( )
(a>0,b>0)的渐近线与抛物线y=x2 +1相切,则该双曲线的离心率等于( )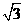 B.2 C.
B.2 C.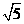 D.
D.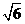
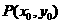 ,则切线的斜率为
,则切线的斜率为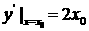 .
.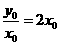 又
又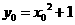
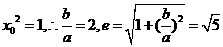 .
. 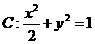 的右焦点为
的右焦点为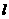 ,点
,点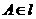 ,线段
,线段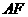 交
交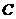 于点
于点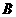 ,若
,若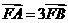 ,则
,则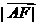 =( )
=( )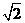 B.
2
C.
B.
2
C.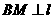 于M,并设右准线
于M,并设右准线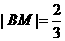 .又由椭圆的第二定义,得
.又由椭圆的第二定义,得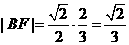
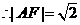 .故选A
.故选A 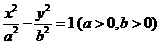 的右顶点
的右顶点 作斜率为
作斜率为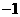 的直线,该直线与双曲线的两条渐近线的交点分别为
的直线,该直线与双曲线的两条渐近线的交点分别为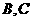 .若
.若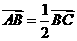 ,则双曲线的离心率是 ( )
,则双曲线的离心率是 ( ) 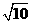
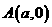 ,则直线方程为
,则直线方程为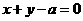 ,直线与两渐近线的交点为B,C,
,直线与两渐近线的交点为B,C,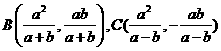 则有
则有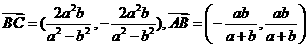 ,因
,因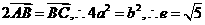 .
.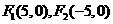 ,双曲线上的一点
,双曲线上的一点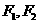 的距离差的绝对值等于
的距离差的绝对值等于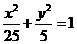 共焦点且过点
共焦点且过点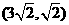 的双曲线的方程;
的双曲线的方程;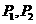 坐标分别为
坐标分别为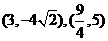 ,求双曲线的标准方程。
,求双曲线的标准方程。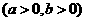 ,
,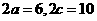 ,∴
,∴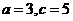 ,∴
,∴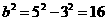 。
。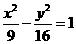 ;
;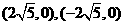 ,可以设双曲线的方程为
,可以设双曲线的方程为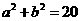 。
。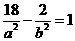 。
。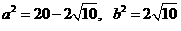 ,所以
,所以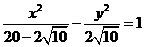 。
。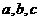 之间的关系。
之间的关系。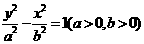 ①;
①;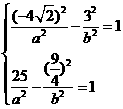
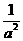 和
和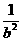 看着整体,解得
看着整体,解得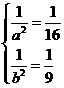 ,
,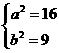 即双曲线的标准方程为
即双曲线的标准方程为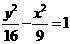 。
。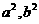 即可得到双曲线的方程,没有必要求出
即可得到双曲线的方程,没有必要求出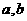 的值;在求解的过程中也可以用换元思想,可能会看的更清楚
的值;在求解的过程中也可以用换元思想,可能会看的更清楚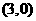 ,且焦距与虚轴长之比为
,且焦距与虚轴长之比为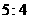 ,则双曲线的标准方程是____________________.
,则双曲线的标准方程是____________________.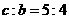 ,解得
,解得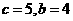 ,则双曲线的标准方程是
,则双曲线的标准方程是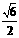 的是
的是 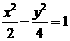 B.
B.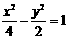 C.
C.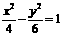 D.
D.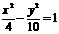
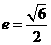 得
得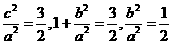 ,选B.
,选B.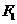 和
和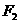 为双曲线
为双曲线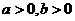 )的两个焦点, 若
)的两个焦点, 若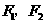 ,
,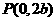 是正三角形的三个顶点,则双曲线的离心率为
是正三角形的三个顶点,则双曲线的离心率为 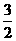 B.
B.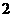 C.
C.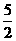 D.3
D.3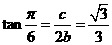 有
有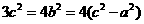 ,则
,则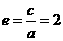 ,故选B.
,故选B.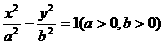 的虚轴长为2,焦距为
的虚轴长为2,焦距为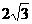 ,则双曲线的渐近线方程为(
)
,则双曲线的渐近线方程为(
)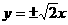 B .
B .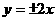 C .
C .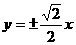 D.
D.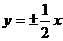
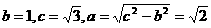 ,因为双曲线的焦点在x轴上,故渐近线方程为
,因为双曲线的焦点在x轴上,故渐近线方程为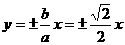
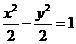 的准线过椭圆
的准线过椭圆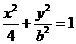 的焦点,则直线
的焦点,则直线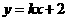 与椭圆至多有一个交点的充要条件是( )
与椭圆至多有一个交点的充要条件是( )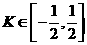 B.
B. 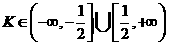
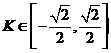 D.
D. 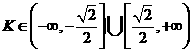
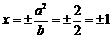
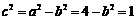 即
即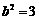 所以方程是
所以方程是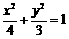
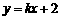 可得
可得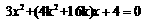 由
由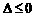 可解得A.
可解得A.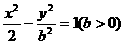 的左、右焦点分别是
的左、右焦点分别是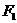 、
、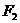 ,其一条渐近线方程为
,其一条渐近线方程为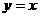 ,点
,点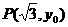 在双曲线上.则
在双曲线上.则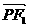 ·
·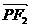 =( )
=( )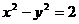 ,于是两焦点坐标分别是(-2,0)和(2,0),且
,于是两焦点坐标分别是(-2,0)和(2,0),且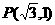 或
或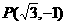 .不妨去
.不妨去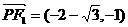 ,
,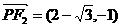 .
.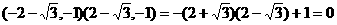
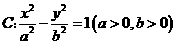 的右焦点为
的右焦点为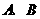 两点,若
两点,若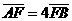 ,则
,则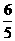 B.
B. 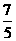 C.
C.
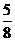 D.
D.
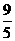
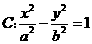 的右准线为
的右准线为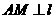 于
于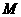 ,
,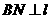 于
于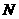 ,
, 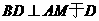 ,由直线AB的斜率为
,由直线AB的斜率为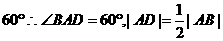 ,
,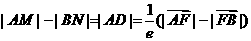
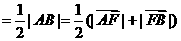 .
.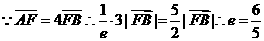 .
.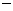 2),求它的标准方程
2),求它的标准方程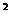 =4x,y
=4x,y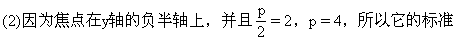
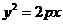 的焦点与椭圆
的焦点与椭圆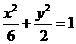 的右焦点重合,则
的右焦点重合,则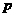 的值为( )
的值为( )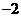 B.
B.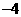 D.
D.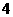
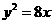 的准线方程是( )
的准线方程是( )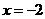 (B)
(B) 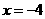 (C)
(C) 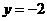 (D)
(D)
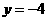
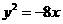 的焦点坐标是( )
的焦点坐标是( )
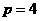 ,故选D;
,故选D;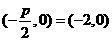 ,故选B.
,故选B.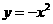 上的点到直线
上的点到直线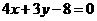 距离的最小值是( )
距离的最小值是( )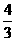 B.
B.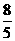 D.
D.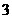
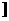 C.[0,2] D.(0,2)
C.[0,2] D.(0,2)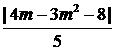 ,当m=
,当m=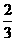 时,取得最小值为
时,取得最小值为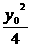 ,y0),
,y0),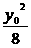 恒成立.而2+
恒成立.而2+