1攻略之一--学会数学建模分析的步骤
应用型问题解决的关键是把实际问题抽象为数学问题来解决,完成整个解题过程大体可以分为四个步骤:
(1)读题:读懂和深刻理解,译为数学语言,找出主要关系;
(2)建模:把主要关系近似化、形式化,抽象成数学问题;
(3)求解:化归为常规问题,选择合适的数学方法求解;
(4)评价:对结果进行验证或评估,对错误加以调节,最后将结果应用于现实,作出解释或验证。
[例1](2009山东卷理)(本小题满分12分)
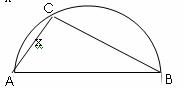
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧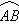 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在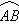 的中点时,对城A和城B的总影响度为0.065。
的中点时,对城A和城B的总影响度为0.065。
(1)将y表示成x的函数;
(2)讨论(1)中函数的单调性,并判断弧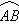 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
解析:(1)如图,由题意知AC⊥BC,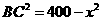 ,
,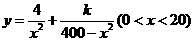
其中当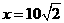 时,y=0.065,所以k=9
时,y=0.065,所以k=9
所以y表示成x的函数为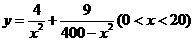
(2)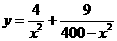 ,
,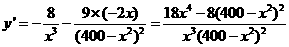 ,令
,令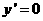 得
得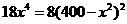 ,所以
,所以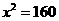 ,即
,即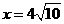 ,当
,当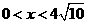 时,
时, 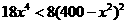 ,即
,即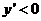 所以函数为单调减函数,当
所以函数为单调减函数,当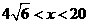 时,
时, 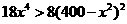 ,即
,即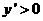 所以函数为单调增函数,所以当
所以函数为单调增函数,所以当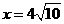 时,即当C点到城A的距离为
时,即当C点到城A的距离为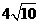 时,函数
时,函数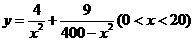 有最小值。
有最小值。
[点评]本题主要考查了函数在实际问题中的应用,运用待定系数法求解函数解析式的 能力和运用换元法和基本不等式研究函数的单调性等问题.
2攻略之二--掌握数学建模分析的具体方法
注意总结解高中数学应用题的基本模式,以便在解题过程中能尽快找到解题方法,达到“生中见熟”的效果。如行程、工程、浓度等问题可转化为方程(组)或不等式(组)的求解问题;平均增长率问题可转化为求解数列和指数方程(不等式)问题;用料最省、造价最低、容积(面积)最值问题可转化为函数、线性规划最值问题;应用题与平面图形有关时,如拱桥设计可转化为二次曲线,航海、测量问题转化为三角函数问题等;一般可采用关系分析法、列表分析法、图像分析法等方法、分析题目的层次、领会关键词语,弄清题图关系、重视条件转译,准确建模。
[例2](2001年高考试题)(旅游业的投入产出问题)从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年投入将比上年减少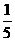 ,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
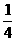 。
。
(1)设 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为
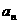 万元,旅游业总收入为
万元,旅游业总收入为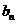
 万元,写出它们的表达式;
万元,写出它们的表达式;
(2)至少经过几年旅游业的总收入才能超过总投入?
解析:在研究旅游业的投入产出问题时,根据“本年度投入800万元,以后每年投入将比上年减少 ”和“旅游业收入每年会比上年增加
”和“旅游业收入每年会比上年增加 ”,其投入资金数列和收入(产出)数列均为等比数列,注意题目“设
”,其投入资金数列和收入(产出)数列均为等比数列,注意题目“设 年内(本年度为第一年)总投入
年内(本年度为第一年)总投入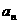 为
为 万元,旅游业总收入为
万元,旅游业总收入为
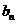 万元”中的“
万元”中的“ 年内”说明“
年内”说明“
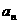 ”、“
”、“
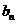 ”表示等比数列的前
”表示等比数列的前 项和。
项和。
建立数学模型:(1)第n 年的投入与收入资金数列列表如下
年的投入与收入资金数列列表如下
|
第n年 |
第n年投入资金(万元) |
第n年旅游收入(万元) |
|
1 |
800 |
400 |
|
2 |
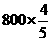 |
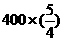 |
|
3 |
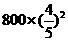 |
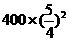 |
|
4 |
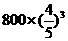 |
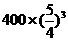 |
|
………… |
……… |
………. |
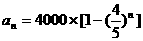
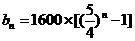 (2)略
(2)略
[点评]通过列表分析,数学模型一目了然,不同的问题要灵活选用不同的分析方法。
3攻略之二--注重数形结合逐步翻译条件
应用性问题往往有大段的文字描述,在解答过程中要真读题、审题,通过审题领会其中的数的本质,并且要养成边读题边画图的习惯,树立数形结合意识,把抽象繁琐的文字叙述,逐步翻译为具体直观的图形关系。
[例3](2009辽宁卷)如图, 都在同一个与水平面垂直的平面内,
都在同一个与水平面垂直的平面内,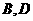 为两岛上的两座灯塔的塔顶。测量船于水面
为两岛上的两座灯塔的塔顶。测量船于水面 处测得
处测得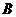 点和
点和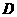 点的仰角分别为
点的仰角分别为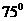 ,
,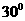 ,于水面
,于水面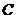 处测得
处测得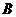 点和
点和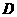 点的仰角均为
点的仰角均为 ,
,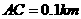 。试探究图中
。试探究图中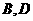 间距离与另外哪两点距离相等,然后求
间距离与另外哪两点距离相等,然后求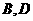 的距离(计算结果精确到0.01km,
的距离(计算结果精确到0.01km,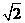
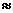 1.414,
1.414,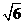
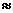 2.449)
2.449)
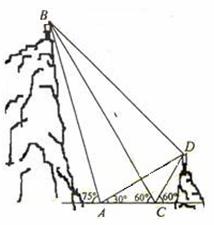
解析:在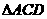 中,
中,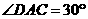 ,
,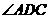 =60°-
=60°-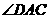 =30°,
=30°,
所以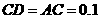
又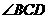 =180°-60°-60°=60°,
=180°-60°-60°=60°,
故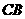 是
是 底边
底边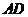 的中垂线,所以
的中垂线,所以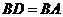 ,
,
在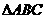 中,
中,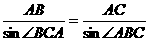 ,
,
即AB=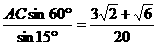
因此,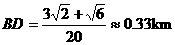
故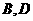 的距离约为0.33km。
的距离约为0.33km。
[点评]对于这类问题在解题过程中,要明确相关的术语概念,如方位角\仰角\俯角等概念,这时顺利解出题目的前提.
4攻略之四--注意语言表达的完整性
数学应用题的求解不同于一般的数学运算题,有人比喻它是数学中的小作文,因此解数学应用题要做到“有头有尾”,把问题中的普通语言转化为数学语言,引入变量与字母,画出图形,将数学建模的过程详细地写出来,建立数学模型后,要准确地求解,并注意计量单位的一致,最后对于所得数据不仅要思考或检验是否与实际吻合,而且要给出完整的答案。
 (单位:米)与时间
(单位:米)与时间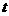 (单位:秒)满足函数关系式
(单位:秒)满足函数关系式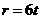 ,则在2秒末扰动水面面积的变化率为 ( )
,则在2秒末扰动水面面积的变化率为 ( ) B.
B. 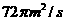 C.
C. 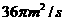 D.
D. 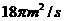
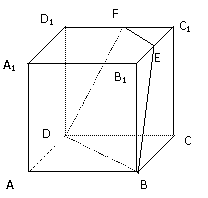 (3)求直线A1D与平面BDFE所成的角
(3)求直线A1D与平面BDFE所成的角
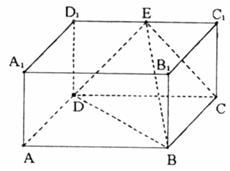 (本小题满分12分)在长方体ABCD-
(本小题满分12分)在长方体ABCD-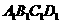 中,AB=2,
中,AB=2,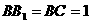 ,E为
,E为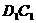 的中点,连结ED,EC,EB和DB。
的中点,连结ED,EC,EB和DB。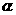 ∥平面b,A、B在
∥平面b,A、B在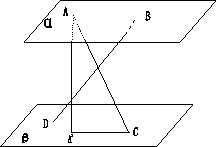 ⑴ AC、BD在平面
⑴ AC、BD在平面