摘要:. 如图.直三棱柱ABC-A1B1C1中.AB⊥AC,D.E分别为AA1.B1C的中点.DE⊥平面BCC1 (Ⅰ)证明:AB=AC (Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小 解析:本题考查线面垂直证明线面夹角的求法.第一问可取BC中点F.通过证明AF⊥平面BCC1,再证AF为BC的垂直平分线.第二问先作出线面夹角.即证四边形AFED是正方形可证平面DEF⊥平面BDC.从而找到线面夹角求解.此题两问也可建立空间直角坐标系利用向量法求解. 解法一:(Ⅰ)取BC中点F.连接EF.则EF.从而EFDA. 连接AF.则ADEF为平行四边形.从而AF//DE.又DE⊥平面.故AF⊥平面.从而AF⊥BC.即AF为BC的垂直平分线.所以AB=AC. (Ⅱ)作AG⊥BD.垂足为G.连接CG.由三垂线定理知CG⊥BD.故∠AGC为二面角A-BD-C的平面角.由题设知.∠AGC=600.. 设AC=2.则AG=.又AB=2.BC=.故AF=. 由得2AD=.解得AD=. 故AD=AF.又AD⊥AF.所以四边形ADEF为正方形. 因为BC⊥AF.BC⊥AD.AF∩AD=A.故BC⊥平面DEF.因此平面BCD⊥平面DEF. 连接AE.DF.设AE∩DF=H.则EH⊥DF.EH⊥平面BCD. 连接CH.则∠ECH为与平面BCD所成的角.. 因ADEF为正方形.AD=.故EH=1.又EC==2. 所以∠ECH=300.即与平面BCD所成的角为300. 解法二: (Ⅰ)以A为坐标原点.射线AB为x轴的正半轴.建立如图所示的直角坐标系A-xyz. 设B.D.则,E(..c). 于是=(..0).=.由DE⊥平面知DE⊥BC. =0.求得b=1.所以 AB=AC. (Ⅱ)设平面BCD的法向量则 又=. =,故 令x=1, 则y=1, z=,=(1,1, ). 又平面的法向量= 由二面角为60°知.=60°. 故 °.求得 于是 . . ° 所以与平面所成的角为30°
网址:http://m.1010jiajiao.com/timu3_id_536645[举报]
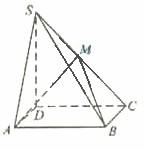
(2009全国卷Ⅰ文)(本小题满分12分)(注决:在试题卷上作答无效)
如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,点
,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 。
。
(I)证明:![]() 是侧棱
是侧棱![]() 的中点;
的中点;

![]() 求二面角
求二面角![]() 的大小。(同理18)
的大小。(同理18)
(2009全国卷Ⅰ文)(本小题满分12分)(注决:在试题卷上作答无效)
如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,点
,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 。
。
(I)证明:![]() 是侧棱
是侧棱![]() 的中点;
的中点;
![]() 求二面角
求二面角![]() 的大小。(同理18)
的大小。(同理18)