20、本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查数形
结合思想、化归与转化思想、分类与整合思想。满分14分。
解法一:
(Ⅰ)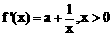 ………………………………………………………… 2分
………………………………………………………… 2分
当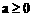 ,
,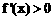 ,函数
,函数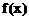 在
在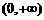 内是增函数,
内是增函数,
∴函数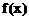 没有极值。 …………………………………………………… 3分
没有极值。 …………………………………………………… 3分
当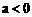 时,令
时,令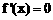 ,得
,得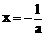 。
。
当 变化时,
变化时,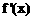 与
与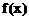 变化情况如下表:
变化情况如下表:
 |
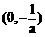 |
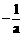 |
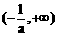 |
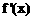 |
+ |
0 |
- |
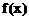 |
单调递增 |
极大值 |
单调递减 |
∴当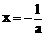 时,
时,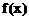 取得极大值
取得极大值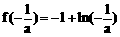 。
。
综上,当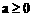 时,
时,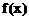 没有极值;
没有极值;
当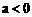 时,
时,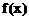 的极大值为
的极大值为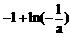 ,没有极小值。 …………… 5分
,没有极小值。 …………… 5分
(Ⅱ)(ⅰ)设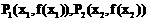 是曲线
是曲线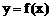 上的任意两点,要证明
上的任意两点,要证明
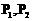 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点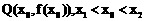 ,使得
,使得
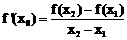 ,且点
,且点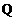 不在
不在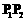 上。 ………………………… 7分
上。 ………………………… 7分
∵错误!不能通过编辑域代码创建对象。,即证存在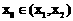 ,使得
,使得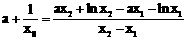 ,即
,即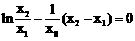 成立,且点
成立,且点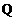 不在
不在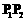 上。 ………………… 8分
上。 ………………… 8分
以下证明方程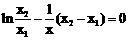 在
在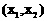 内有解。
内有解。
记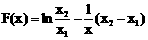 ,则
,则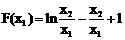 。
。
令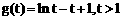 ,
,
∴错误!不能通过编辑域代码创建对象。,
∴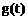 在
在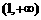 内是减函数,∴
内是减函数,∴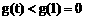 。
。
取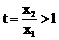 ,则
,则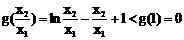 ,即
,即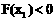 。…… 9分
。…… 9分
同理可证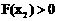 。∴
。∴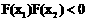 。
。
∴函数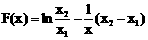 在
在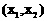 内有零点。
内有零点。
即方程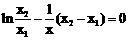 在
在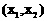 内有解
内有解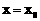 。……………… 10分
。……………… 10分
又对于函数 取
取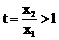 ,则
,则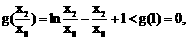
可知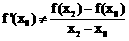 ,即点Q不在
,即点Q不在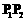 上。
上。
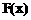 是增函数,∴
是增函数,∴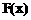 的零点是唯一的,
的零点是唯一的,
即方程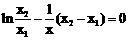 在
在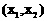 内有唯一解。
内有唯一解。
综上,曲线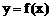 上任意一条弦均有伴随切线,并且伴随切线是唯一的。
上任意一条弦均有伴随切线,并且伴随切线是唯一的。
…………………………………………………………………………… 11分
(ⅱ)取曲线C: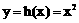 ,则曲线
,则曲线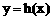 的任意一条弦均有
的任意一条弦均有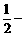 伴随切线。
伴随切线。
证明如下:
设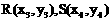 是曲线C上任意两点
是曲线C上任意两点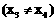 ,
,
则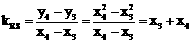 ,
,
又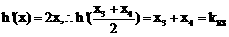 ,
,
即曲线C: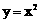 的任意一条弦均有
的任意一条弦均有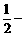 伴随切线。 ………………… 14分
伴随切线。 ………………… 14分
注:只要考生给出一条满足条件的曲线,并给出正确证明,均给满分。若只给曲
线,没有给出正确的证明,不给分。
解法二:
(Ⅰ)同解法一。
(Ⅱ)(ⅰ)设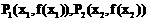 是曲线
是曲线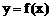 上的任意两点,要证明
上的任意两点,要证明
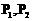 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点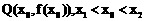 ,使得
,使得
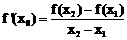 ,且点
,且点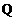 不在
不在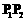 上。 …………………………… 7分
上。 …………………………… 7分
∵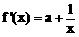 ,即证存在
,即证存在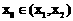 ,使得
,使得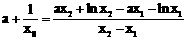 ,
,
即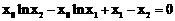 成立,且点
成立,且点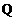 不在
不在 上。 …………… 8分
上。 …………… 8分
以下证明方程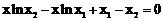 在
在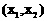 内有解。
内有解。
设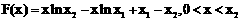 。
。
则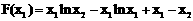 。
。
记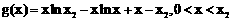 ,
,
∴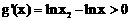 ,
,
∴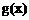 在
在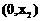 内是增函数,
内是增函数,
∴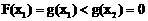 。 …………………………………………… 9分
。 …………………………………………… 9分
同理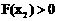 。
。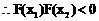 。
。
∴方程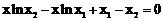 在
在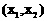 内有解
内有解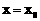 。 ………… 10分
。 ………… 10分
又对于函数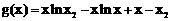 ,
,
∵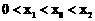 ,
,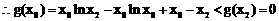 ,
,
可知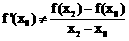 ,即点Q不在
,即点Q不在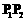 上。
上。
又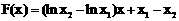 在
在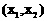 内是增函数,
内是增函数,
∴方程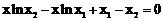 在
在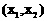 内有唯一解。
内有唯一解。
综上,曲线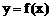 上任意一条弦均有伴随切线,并且伴随切线是唯一的。
上任意一条弦均有伴随切线,并且伴随切线是唯一的。
…………………………………………………………………………… 11分
(ⅱ)同解法一。
17、本小主要考查概率、统计等基础知识,考查数据处理能力、运算求解能力以及应用数学知识分析和解决实际问题的能力。满分13分。
解:(Ⅰ) 作出茎叶图如下:
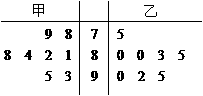
……………………………………… 4分
(Ⅱ) 派甲参赛比较合适。理由如下:
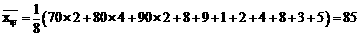 ,
,
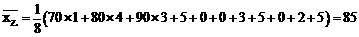 ,
,
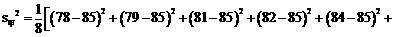
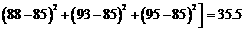 ,
,
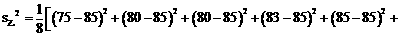
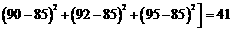
∵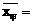
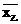 ,
,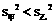 ,
,
∴甲的成绩较稳定,派甲参赛比较合适。 ……………………………… 8分
注:本小题的结论及理由均不唯一,如果考生能从统计学的角度分析,给出其他合理回答,同样给分。如
派乙参赛比较合适。理由如下:
从统计的角度看,甲获得85分以上(含85分)的概率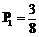 ,
,
乙获得85分以上(含85分)的概率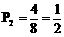 。
。
∵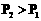 ,∴派乙参赛比较合适。
,∴派乙参赛比较合适。
(Ⅲ) 记“甲同学在一次数学竞赛中成绩高于80分”为事件A,
则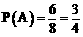 。 ………………………………………………………… 9分
。 ………………………………………………………… 9分
随机变量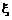 的可能取值为0、1、2、3,且
的可能取值为0、1、2、3,且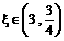 。
。
∴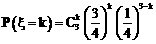 ,
,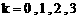 。
。
所以变量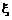 的分布列为:
的分布列为:
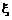 |
0 |
1 |
2 |
3 |
|
P |
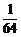 |
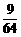 |
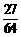 |
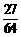 |
…………………………………………………………………………… 11分
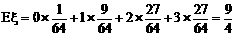 。
。
(或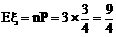 ) ……………………………………………… 13分
) ……………………………………………… 13分
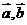 ,则
,则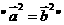 是
是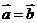 的
的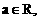 矩阵
矩阵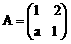 对应的线性变换把点
对应的线性变换把点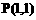 变成
变成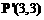 ,求矩阵A的特征值
,求矩阵A的特征值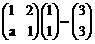 ,得
,得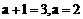 ………………………………………… 2分
………………………………………… 2分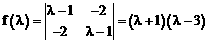 。 …………… 4分
。 …………… 4分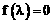 ,得矩阵A的特征值
,得矩阵A的特征值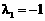 ,
,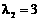 。 ……………………… 5分
。 ……………………… 5分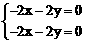 ,得一个非零解
,得一个非零解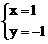 。
。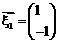 是矩阵A的属于特征值
是矩阵A的属于特征值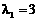 ,解相应的线性方程组
,解相应的线性方程组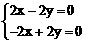 ,得一个非零解
,得一个非零解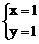 。
。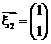 是矩阵A的属于特征值
是矩阵A的属于特征值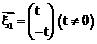 ,
,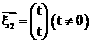 即可。
即可。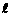 经过点
经过点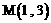 ,且倾斜角为
,且倾斜角为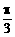 ,圆C的参数方程为
,圆C的参数方程为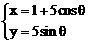 (
(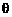
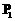 、
、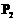 两点,求
两点,求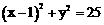 。……………………… 2分
。……………………… 2分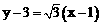 ,即
,即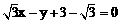 。 ……………… 3分
。 ……………… 3分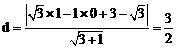 , ……………………… 5分
, ……………………… 5分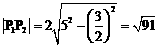 。 …………………………………………… 7分
。 …………………………………………… 7分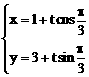 ,即
,即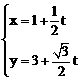 (t为参数),………… 1分
(t为参数),………… 1分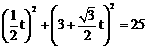 ,即
,即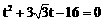 。 ………………………… 4分
。 ………………………… 4分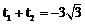 ,
,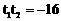 ,………………………………………………… 5分
,………………………………………………… 5分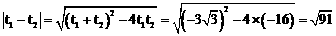 ,
,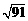 。 …………………………………………… 7分
。 …………………………………………… 7分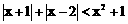 。
。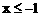 时,原不等式可化为:
时,原不等式可化为: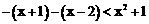 ,解得:
,解得: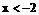 或
或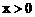 。
。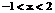 时,原不等式可化为:
时,原不等式可化为: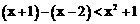 ,解得:
,解得: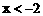 或
或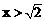
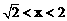 。 ……………………………………………………………… 4分
。 ……………………………………………………………… 4分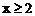 时,原不等式可化为:
时,原不等式可化为: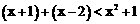 ,解得
,解得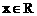 。
。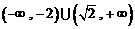 。 ………………… 7分
。 ………………… 7分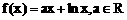
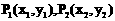 ,如果存在曲线上的点
,如果存在曲线上的点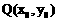 ,
,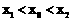 ,使得曲线在点
,使得曲线在点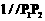 ,则称
,则称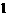 为弦
为弦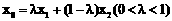 时,又称
时,又称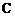 的方程为
的方程为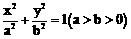 。 ………………………… 1分
。 ………………………… 1分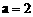 ,
,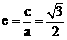 ,∴
,∴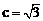 ,
,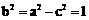 。 ……………… 4分
。 ……………… 4分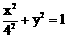 。 ……………………………………… 5分
。 ……………………………………… 5分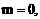 得
得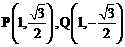 ,
,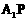 的方程是
的方程是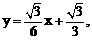 直线
直线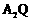 的方程是
的方程是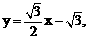
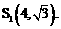 ……………………………………………………… 7分
……………………………………………………… 7分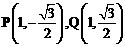 ,由对称性可知交点为
,由对称性可知交点为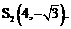
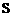 在同一条直线上,则直线只能为
在同一条直线上,则直线只能为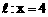 。 ………………… 8分
。 ………………… 8分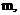 直线
直线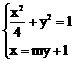
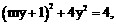 即
即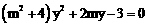 ,
,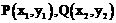 ,则
,则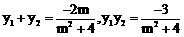 。………… 9分
。………… 9分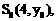 由
由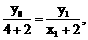 得
得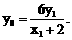
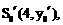 由
由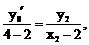 得
得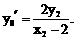 ……… 10分
……… 10分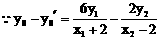
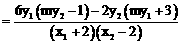
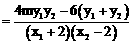
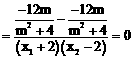 , …………………………………………… 12分
, …………………………………………… 12分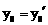 ,即
,即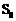 与
与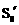 重合,
重合, 变化时,点
变化时,点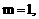 得
得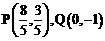 ,
,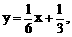 直线
直线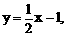 交点为
交点为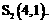
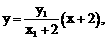
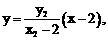
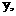 得
得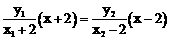 …………………………………… ①
…………………………………… ①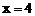 时,①式恒成立。
时,①式恒成立。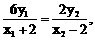
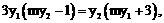 即证
即证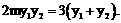 ……………… ②
……………… ②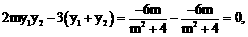 ∴②式恒成立。
∴②式恒成立。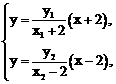 得
得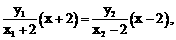 ………………… 9分
………………… 9分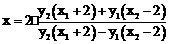
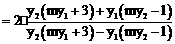
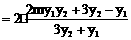
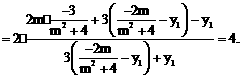 ……………………………… 12分
……………………………… 12分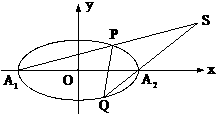 已知椭圆C的离心率
已知椭圆C的离心率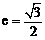 ,长轴的左右端点分
,长轴的左右端点分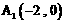 ,
,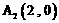 。
。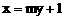 与椭圆C交于P、Q两
与椭圆C交于P、Q两 交于点S。试问:当
交于点S。试问:当 想象能力,推理论证能力和运算求解能力。满分13分。
想象能力,推理论证能力和运算求解能力。满分13分。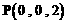 ,
, ,
,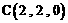 ,
,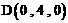 。
。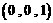 ,
,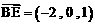 ,
,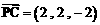 ,
,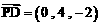 。
。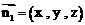 是平面PCD的法向量。
是平面PCD的法向量。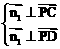 ,即
,即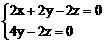
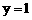 ,得
,得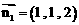 为平面PCD的一个法向量。 ……………… 6分
为平面PCD的一个法向量。 ……………… 6分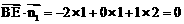 ,∴
,∴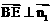 , ……………………… 7分
, ……………………… 7分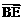 ∥平面PCD。又BE
∥平面PCD。又BE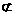 平面PCD,∴BE∥平面PCD。 ………… 8分
平面PCD,∴BE∥平面PCD。 ………… 8分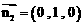 …… 11分
…… 11分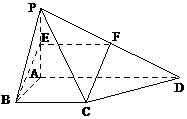 ∴
∴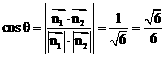 。 ………………………………………… 13分
。 ………………………………………… 13分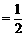 AD,∴EF∥BC,且EF
AD,∴EF∥BC,且EF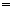 BC,
BC,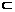 平面PCD,BE
平面PCD,BE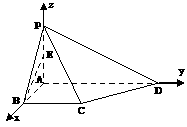 则
则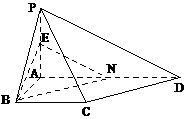 ∴
∴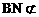 平面PCD,∴BN∥平面PCD。 ……………………………… 6分
平面PCD,∴BN∥平面PCD。 ……………………………… 6分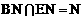 ,∴平面BEN∥平面PCD。……………………………… 7分
,∴平面BEN∥平面PCD。……………………………… 7分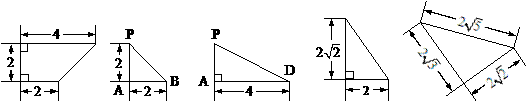
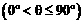 ,求
,求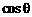
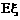 。
。