0 52841 52849 52855 52859 52865 52867 52871 52877 52879 52885 52891 52895 52897 52901 52907 52909 52915 52919 52921 52925 52927 52931 52933 52935 52936 52937 52939 52940 52941 52943 52945 52949 52951 52955 52957 52961 52967 52969 52975 52979 52981 52985 52991 52997 52999 53005 53009 53011 53017 53021 53027 53035 447348
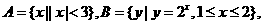 则
则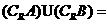 ( )
( )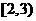 B.
B.
 C.
C. D.
D.
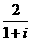 的模的值为( )
的模的值为( )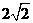 B.2 C.
B.2 C.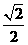 D.
D.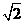
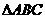 的内角
的内角 、
、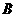 、
、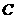 所对的边分别为
所对的边分别为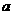 、
、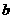 、
、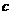 ,向量
,向量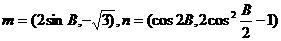 ,且
,且 ∥
∥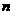 ,
,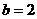 ,求
,求 的最大值.
的最大值.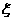 的数学期望.
的数学期望.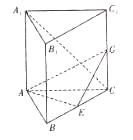 如图,在直三棱柱
如图,在直三棱柱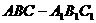 中,
中,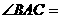 90°,
90°,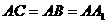 ,
,
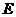 是
是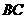 的中点.
的中点.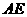 与
与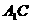 所成的角;
所成的角;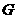 为
为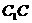 上一点,且
上一点,且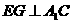 ,求二面角
,求二面角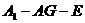 的大小.
的大小.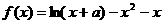 在
在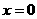 处取得极值.
处取得极值.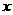 的方程
的方程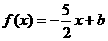 在区间
在区间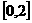 上恰有两个不同的实数根,求实
上恰有两个不同的实数根,求实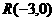 ,点
,点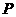 在
在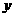 轴上,点
轴上,点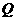 在
在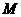 在直线
在直线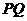 上,且
上,且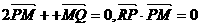 .
.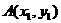 、
、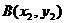 为轨迹
为轨迹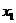 >1,
>1, 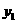 >0,
>0,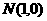 ,求实数
,求实数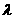 ,
,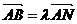 ,且
,且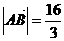 .
.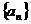 、
、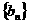 满足
满足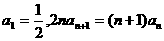 ,且
,且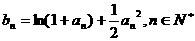 .
.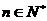 ,证明
,证明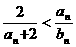 成立;
成立;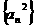 、
、 、
、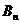 ,证明:
,证明: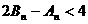 .
.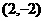 为圆心并且与圆
为圆心并且与圆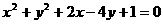 相外切的圆的方程是 .
相外切的圆的方程是 .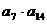 的最大值为
.
的最大值为
. 为坐标原点,点
为坐标原点,点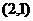 ,若
,若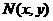 满足不等式组:
满足不等式组: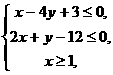 则
则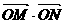 的最大值为
.
的最大值为
.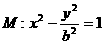 的左顶点
的左顶点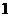 的直线
的直线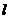 ,若
,若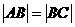 ,则双曲线
,则双曲线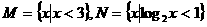 ,则
,则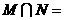
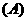
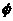 .
. 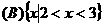 .
. 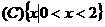 .
. 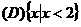 .
.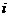 为虚数单位,则
为虚数单位,则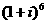 展开式中的第三项为
展开式中的第三项为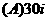 .
. 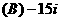 .
.
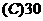 .
.
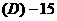 .
.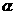 、
、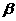 是不同的平面,
是不同的平面,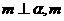 ∥
∥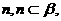 则
则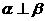 .
. 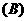 若
若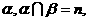 则
则 若
若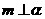 ,则
,则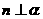 .
.
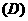 若
若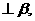 则
则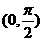 上为增函数且以
上为增函数且以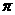 为周期的函数是
为周期的函数是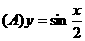 .
. 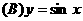 .
. 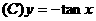 .
. 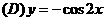 .
.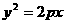 的焦点与椭圆
的焦点与椭圆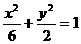 的右焦点重合,则
的右焦点重合,则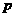 的值为
的值为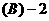 .
.
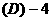 .
.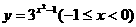 的反函数是
的反函数是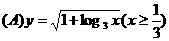 .
.
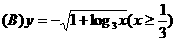 .
.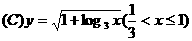 .
. 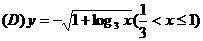 .
.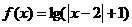 ;②
;②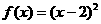 ;③
;③ .有如下三个命题:
.有如下三个命题: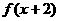 是偶函数;
是偶函数;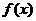 在
在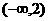 上是减函数,在
上是减函数,在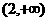 上是增函数;
上是增函数;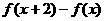 在
在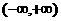 上是增函数.
上是增函数.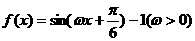 的导数
的导数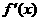 最大值为3,则
最大值为3,则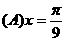 .
.
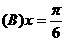 .
.
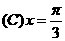 .
. 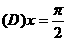 .
.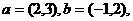 若
若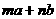 与
与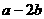 共线,则
共线,则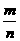 等于
等于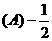 .
.
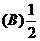 .
.
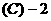 .
.
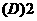 .
.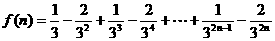 (其中
(其中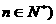 ,则
,则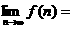
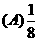 .
.
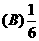 .
.
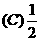 .
.
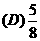 .
.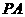 、
、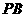 、
、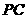 两两成60°角,且分别与球
两两成60°角,且分别与球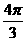 ,则
,则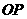 的长度为
的长度为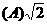 .
.
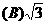 .
.
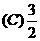 .
.
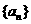 满足
满足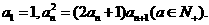
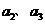 及
及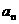 ;
;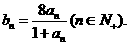 求证
求证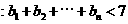
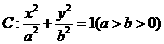 过点
过点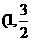 ),且离心率
),且离心率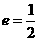 .
.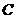 的方程;
的方程;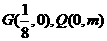 若椭圆
若椭圆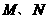 ,使
,使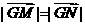 ,且
,且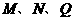 共线,求实数
共线,求实数 的取值范围。
的取值范围。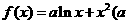 为实常数).
为实常数).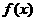 在区间
在区间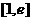 上的最小值及相应的
上的最小值及相应的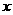 值;
值;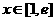 ,使得
,使得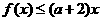 成立,求实数
成立,求实数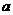 的取值范围。
的取值范围。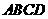 中,
中,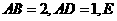 是
是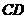 的中点,以
的中点,以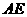 为折痕将
为折痕将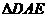 向
向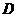 为
为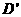 ,且平面
,且平面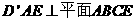
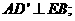
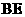 与平面
与平面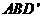 所成角的大小。
所成角的大小。