摘要:本小题主要考查函数.导数等基础知识.考查推理论证能力.运算求解能力.考查数形 结合思想.化归与转化思想.分类与整合思想.满分14分. 解法一: (Ⅰ) ---------------------- 2分 当..函数在内是增函数. ∴函数没有极值. -------------------- 3分 当时.令.得. 当变化时.与变化情况如下表: + 0 - 单调递增 极大值 单调递减 ∴当时.取得极大值. 综上.当时.没有极值, 当时.的极大值为.没有极小值. ----- 5分 设是曲线上的任意两点.要证明 有伴随切线.只需证明存在点.使得 .且点不在上. ---------- 7分 ∵错误!不能通过编辑域代码创建对象..即证存在.使得.即成立.且点不在上. ------- 8分 以下证明方程在内有解. 记.则. 令. ∴错误!不能通过编辑域代码创建对象.. ∴在内是减函数.∴. 取.则.即.-- 9分 同理可证.∴. ∴函数在内有零点. 即方程在内有解.------ 10分 又对于函数取.则 可知.即点Q不在上. 是增函数.∴的零点是唯一的. 即方程在内有唯一解. 综上.曲线上任意一条弦均有伴随切线.并且伴随切线是唯一的. ----------------------------- 11分 (ⅱ)取曲线C:.则曲线的任意一条弦均有伴随切线. 证明如下: 设是曲线C上任意两点. 则. 又. 即曲线C:的任意一条弦均有伴随切线. ------- 14分 注:只要考生给出一条满足条件的曲线.并给出正确证明.均给满分.若只给曲 线.没有给出正确的证明.不给分. 解法二: (Ⅰ)同解法一. 设是曲线上的任意两点.要证明 有伴随切线.只需证明存在点.使得 .且点不在上. ----------- 7分 ∵.即证存在.使得. 即成立.且点不在上. ----- 8分 以下证明方程在内有解. 设. 则. 记. ∴. ∴在内是增函数. ∴. ----------------- 9分 同理.. ∴方程在内有解. ---- 10分 又对于函数. ∵.. 可知.即点Q不在上. 又在内是增函数. ∴方程在内有唯一解. 综上.曲线上任意一条弦均有伴随切线.并且伴随切线是唯一的. ----------------------------- 11分 (ⅱ)同解法一.
网址:http://m.1010jiajiao.com/timu3_id_529158[举报]
已知函数 其中a>0.
其中a>0.
(I)求函数f(x)的单调区间;
(II)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围;
(III)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间[-3,-1]上的最小值。
【考点定位】本小题主要考查导数的运算,利用导数研究函数的单调性、函数的零点,函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.
查看习题详情和答案>>
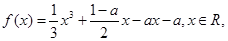 其中a>0.
其中a>0.