摘要: 直线与平面平行的性质定理: [典型例题] [例1] ...求证:. 证:过作 ∴ 过作 ∴ ∴ [例2] .异面.求证过与平行的平面有且仅有一个. 证:存在性.过上一点作直线 确立平面 ∴ 唯一性.假设存在.. ∴ .. 由例1 ∴ 与已知矛盾 ∴ 只有一个 [例3] 为空间一点..异面.过作与.均平行的平面可作个. 个或个.过存在平面.. 过存在平面.. ① 或 个 ② 且 个 可用反证法证明只有一个. [例4] 正方形交正方形于..在对角线.上.且.求证:平面. 证:过作交于 过作交于 . 又∵ 面 [例5] 如图.异面直线....为中点.......求:为中点. 证:连交于.连. ∴ [例6] 三个平面两两相交不共线.求证三条直线交于一点或两两平行. 证:设.. ∴ . (1)若 (2)若 ∴ ..交于一点 [例7] 为 所在平面外一点...且.求证:面. 证:连交于.连. ∴ ∽ ∴ 在中. ∴ 面 [例8] .异面直线.为空间任一点.过作直线与.均相交.这样的直线可以作多少条. 解:.或无数. 过存在唯一个平面 过存在唯一个平面 ① 若或.有无数条 ② 若或.且且 直线不存在 ③ 且.有且只有一条. .过.作平面 ∴ ∴ 连与相交 ∴ 存在与.均相交 假设有两条过的直线.与.均相交 .确立平面 与.各有一个交点 ∴ 同理.与.异面矛盾 ∴ 假设不成立 ∴ 只有一条 [例9] ..两两异面.空间与...均相交的直线有多少条? 证:存在... 存在.. 与.异面.中有无数个点在.外 每一个点可作一条线与.均相交 ∴ 无数条 [模拟试题]
网址:http://m.1010jiajiao.com/timu3_id_517590[举报]
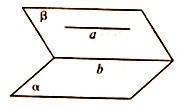 在“直线与平面平行的性质定理”中,如图,如果a∥a,a?β,
在“直线与平面平行的性质定理”中,如图,如果a∥a,a?β,