摘要:(1)解法一:联结AC交DB于点O. ∵ABCD是正方形,∴AC⊥DB. 又PD⊥平面ABCD,AC平面ABCD, ∴AC⊥PD, ∴AC⊥平面PBD. 作OF⊥PB于点F,联结AF,则AF⊥PB. ∴∠OFA就是二面角A-PB-D的平面角. ----2分 ∵PD⊥平面ABCD.AB⊥AD.∴PA⊥AB. 令PD=AD=2.则在RTABC中,PA=,AB=2. ∴PB=,∴. ∴在RTAOF中,sin,∴. ∴二面角A-PB-D的大小为. ----7分 解法二:建立如图所示的直角坐标系. 联结AC,交BD于点O,取PA中点G,联结DG. ∵ABCD是正方形,∴AC⊥DB. 又PD⊥平面ABCD,AC平面ABCD, ∴AC⊥PD, ∴AC⊥平面PBD. ∵PD⊥平面ABCD.AB⊥AD.∴PA⊥AB. ∴AB⊥平面PAD. ∵PD=AD,G为PA中点, ∴GD⊥平面PAB. 故向量分别是平面PBD与平面PAB的法向量. 令PD=AD=2.则A.∴=. ∵P, ∴G,∴=. ----4分 ∴向量的夹角余弦为. ∴,∴二面角A-PB-D的大小为. ---7分 (2)解法一: 当点E是线段PB中点时, 有PC⊥平面ADE. -7分 证明如下: 取PC中点H,联结EH,DH,则有EH∥BC, 又BC∥AD,故有EH∥AD. ∴平面ADE即平面ADHE. ----9分 ∵PD=DC,H为PC中点, ∴PC⊥DH. 又∵PD⊥平面ABCD.AD⊥CD.∴AD⊥PC. ∴PC⊥平面ADHE,即PC⊥平面ADE. ----14分 解法二:建立如图所示的直角坐标系. ∵PD⊥平面ABCD.AD⊥CD.∴AD⊥PC. 设E是线段PB上的一点.令. 令PD=AD=2.则P,B, C, ∴,,. ∴. ∴. 令2(-)=0,得. ∴当,即点E是线段PB中点时,有AE⊥PC. 又∵PD⊥平面ABCD.AD⊥CD.∴AD⊥PC. ∴当点E是线段PB中点时,有PC⊥平面ADE. ----14分
网址:http://m.1010jiajiao.com/timu3_id_517176[举报]
 (2012•许昌县一模)如图所示四边形ABCD内接于E、O,AC交BD于点E,圆的切线DF交BC的延长线于F,CD平分∠BDF
(2012•许昌县一模)如图所示四边形ABCD内接于E、O,AC交BD于点E,圆的切线DF交BC的延长线于F,CD平分∠BDF(Ⅰ)求证:AB•AD=AC•AE
(Ⅱ)若圆的半径为2,弦BD长为2
| 3 |
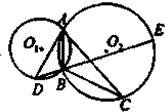 如图,⊙O1与⊙O2相交于点A,B,⊙O1的切线AC交⊙O2于另一点C,⊙O2的切线AD交⊙O1于另一点D,DB的延长线交⊙O2于点E.
如图,⊙O1与⊙O2相交于点A,B,⊙O1的切线AC交⊙O2于另一点C,⊙O2的切线AD交⊙O1于另一点D,DB的延长线交⊙O2于点E.(Ⅰ)求证:AB2=BC•BD;
(Ⅱ)若AB=1,AC=2,AD=
| 2 |
 (2013•东城区一模)如图,已知PA与圆O相切于A,半径OC⊥OP,AC交PO于B,若OC=1,OP=2,则PA=
(2013•东城区一模)如图,已知PA与圆O相切于A,半径OC⊥OP,AC交PO于B,若OC=1,OP=2,则PA=
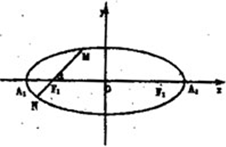 如图,己知椭圆长轴|A1A2|=6.焦距
如图,己知椭圆长轴|A1A2|=6.焦距