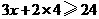5.设学校每天用电量为x度,依题意可得:
110(x+2)>2530
110(x-2)≤2200
解得:21<x≤22,即学校每天用电量应控制在21度-22度范围内。
[解析]设这个学校选派值勤学生x人,共到y个交通路口值勤。
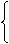 根据题意得
x-4y=78
①
根据题意得
x-4y=78
①
4≤x-8(y-1)<8 ②
由方程①得x=78+4y
代入不等式②得19.5<y≤20.5
根据题意y取20,这时x为158
答:学校派出是158名学生,分到了20个交通路口安排值勤。
解:设需租40座客车x辆,则租50座客车(x-1)辆,最后一辆剩空座[50(x-1)-40x]个.
由题意得0<50(x-1)-40x<20,
解得5<x<7.
∵x为正整数,∴x=6.
∵150×6=900(元),170×(6-1)=850(元).
而900>850. 答:租用50座客车较为合算.
解:(1)根据题意可得:
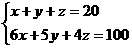 ------------------------------------3分
------------------------------------3分
化简得:y = 20 – 2x, -----------------------------------5分
(2)由题可得: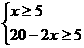 ,解得
,解得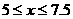 --------7分
--------7分
A、当x = 5时,y = 10, z = 5
B、当x = 6时,y = 8, z = 6
C、当x = 7时,y = 6, z = 7 答:共有三种方案:
A、装运A种荔枝车辆数为5辆,B种荔枝车辆数为10辆,B种荔枝车辆数为5辆;
B、装运A种荔枝车辆数为6辆,B种荔枝车辆数为8辆,B种荔枝车辆数为6辆;
C、装运A种荔枝车辆数为7辆,B种荔枝车辆数为6辆,B种荔枝车辆数为7辆。
(3)A方案的获利:5×6×12+10×5×16+5×4×10=1360(百元)
B方案的获利:6×6×12+8×5×16+6×4×10=1312(百元)
C方案的获利:7×6×12+6×5×16+7×4×10=1264(百元)
答:采用装运A种荔枝车辆数为5辆,B种荔枝车辆数为10辆,B种荔枝车辆数为5辆的方案时,能获得最大利润1360百元。 ---------------------------------------------------12分
(07赤峰市)某私立中学准备招聘教职员工60名,所有员工的月工资情况如下:
|
员工 |
管理人员 |
教学人员 |
|||||
|
人员结构 |
校长 |
副校长 |
部处主任 |
教研组长 |
高级教师 |
中级教师 |
初级教师 |
|
员工人数/人 |
1 |
2 |
4 |
10 |
|
|
3 |
|
每人月工资/元 |
20000 |
17000 |
2500 |
2300 |
2200 |
2000 |
900 |
请根据上表提供的信息,回答下列问题:
(1)如果学校准备招聘“高级教师”和“中级教师”共40名(其他员工人数不变),其中高级教师至少要招聘13人,而且学校对高级、中级教师的月支付工资不超过83000元,按学校要求,对高级、中级教师有几种招聘方案?
(2) (1)中的哪种方案对学校所支付的月工资最少?并说明理由.
(3)在学校所支付的月工资最少时,将上表补充完整,并求所有员工月工资的中位数和众数.
8.某镇组织20辆汽车装运完A、B、C三种荔枝共100吨到外地销售。按计划,20辆汽车都要装运,每辆汽车只能装运同一种荔枝,且必须装满。根据下表提供的信息,解答以下问题:
|
荔 枝 品 种 |
A |
B |
C |
|
每辆汽车运载量(吨) |
6 |
5 |
4 |
|
每吨荔枝获得(百元) |
12 |
16 |
10 |
(1)设装运A种荔枝的车辆数为x,装运B种荔枝的车辆数为y,装运C种荔枝的车辆数为Z,求y与x之间的函数关系式;
(2)如果装运每种荔枝的车辆数都不少于5辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值。
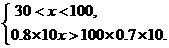
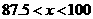 .
. 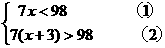 因此不等式组的解集是11<x<14
因此不等式组的解集是11<x<14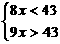 解这个不等式组,得
解这个不等式组,得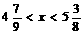

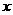 根火腿肠,则关于
根火腿肠,则关于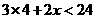 B.
B.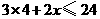 C.
C.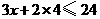 D.
D.