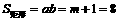3、随机抽取某城市30天的空气质量状况统计如下表:
|
污染指数(ω) |
40 |
70 |
90 |
110 |
120 |
140 |
|
天数(t) |
3 |
5 |
10 |
7 |
4 |
1 |
其中,ω≤50时,空气质量为优;50<ω≤100时,空气质量为良;100<ω≤150时,空气质量为轻微污染,估计该城市一年(以365天计)中有多少天空气质量达到良以上。
2、南方A市欲将一批容易变质的水果运往B市销售,共有飞机、火车、汽车三种运输方式,现只有可选择其中的一种,这三种运输方式的主要参考数据如下表所示:
|
运输工具 |
途中速度 (千米/时) |
途中费用 (元/千米) |
装卸费用 (元) |
装卸时间 (小时) |
|
飞机 |
200 |
16 |
1000 |
2 |
|
火车 |
100 |
4 |
2000 |
4 |
|
汽车 |
50 |
8 |
1000 |
2 |
这批水果在运输(包括装卸)过程中的损耗为200元/小时,记A、B两市间的距离为x千米。(1)如果用W1、W2、W3分别表示使用飞机、火车、汽车运输时的总支出费用(包括损耗),求出W1、W2、W3与x之间的函数关系式;(2)应采用哪种运输方式,才能使运输时的总支出费用最小?
例题5、某商店三、四月份同一品牌各种规格的空调销售台数如下表:
 规格 规格台数 月份 |
1匹 |
1.2匹 |
1.5匹 |
2匹 |
|
三月 |
12台 |
20台 |
8台 |
4台 |
|
四月 |
16台 |
30台 |
14台 |
8台 |
根据表中数据回答:(1)商店平均每月销售空调 台。(2)商店出售的各种规格的空调中,众数是 ;
(3)在研究六月份进货时,商店经理决定 匹的空调要多进; 匹的空调要少进。
例题6、有两种药品A和B,已经在甲、乙两家医院做过了临床试验结果如表一所示:
表一
|
|
甲医院 |
乙医院 |
||
|
A药品 |
B药品 |
A药品 |
B药品 |
|
|
试验人数 |
20 |
10 |
80 |
990 |
|
有效人数 |
6 |
2 |
40 |
478 |
|
有效率(%) |
|
|
|
|
(1) 计算表一中的有效率(直接在表中填出结果)。(2)甲、乙两家医院分别根据自己的试验结果,对两种药品的有效率比较,作出的“哪种药效好”的结论是否一致?(3)综合两家医院的试验结果,在表二中作出A和B两种药品的总有效率报告,由此得出什么结论?表二
|
|
A药品 |
B药品 |
|
总试验人数 |
|
|
|
总有效人数 |
|
|
|
总有效率(%) |
|
|
(4)根据上述资料,你认为甲、乙两家医院的试验人数及总试验人数是否合适?(2)和(3)的结论是否科学?
练习题:
|
作物品种 |
每亩地所需职工数 |
每亩地预计产值 |
|
蔬菜 |
1/2 |
1100元 |
|
烟叶 |
1/3 |
750元 |
|
小麦 |
1/4 |
600元 |
1、某市20名下岗职工在近郊承包50亩土地办农场。这些地可种蔬菜、烟叶或小麦,种这几种农作物每亩地所需职工数和产值如下:
请你设计一个种植方案,使每亩地都种上农作物,20名职工都有工作,且使农作物预计总产值最多。
|
|
第一套 |
第二套 |
|
椅子高度xcm |
40.0 |
37.0 |
|
桌子高度ycm |
75.0 |
70.2 |
例题3、为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的。研究表明:假设课桌的高度为ycm,,椅子的高度(不含靠背)为xcm,则y应是x的一次函数关系。下表列出两套符合条件的课桌椅的高度: (1)请确定y与x的函数关系式(不要求写出x的自变量的取值范围);(2)现有一把高为42cm椅子和一张高为78.2Ccm的课桌,它们是否配套?请通过计算说明理由。
例题4、某公司欲请汽车运输公司或火车货运站将60吨火果从A地运到B地。已知汽车和火车从A地到B地的运输路程均为s千米。这两家运输单位在运输过程中,除都要收取运输途中每吨5元的冷藏费外,要收取的其它费用及有关运输资料由下表给出:
|
运输工具 |
行驶速度 (千米/时) |
运费单价 [元/(吨·千米)] |
装卸总费用 (元) |
|
汽车 |
50 |
2 |
3000 |
|
火车 |
80 |
1.7 |
4620 |
(1) 请分别写出这两家运输单位运送这批水果所要的总费用y1(元)和y2(元)(用含s的代数表示)。(2)为减少费用,你认为果品公司应选择哪家运输单位运送这批水果更为分理合算?(说明:“1元/(吨·千米)”表示“每吨每千米1元”)
|
船型 |
每只限载人数(人) |
租金(元) |
|
大船 |
5 |
3 |
|
小船 |
3 |
2 |
例题2、某公司决定组织48名员工双休日到附近一水上公园坐船游园,公司先派一人去了解船只的租金情况。这个人看到的租金价格如下:
那么怎样设计方案才能使所付租金最少?(严禁超载)
 时间
时间收盘价(元/股) 名称 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
|
甲 |
12 |
12.5 |
12.9 |
12.45 |
12.75 |
|
乙 |
13.5 |
13.3 |
13.9 |
13.4 |
13.15 |
例题1、下表是某一周甲、乙两种股票每天的收盘价:(收盘价是指股票每天交易结束时的价格)
某人在该周内持有若干股甲、乙两种股票,若按照两种股票每天的收盘价计算(不计手续费、税费等),该人账户上星期二比星期一多获利200元,星期三比星期二多获利1300元。试问该人持有甲、乙股票各多少股?
24]正方形提供剪切可以拼成三角形。方法如下:
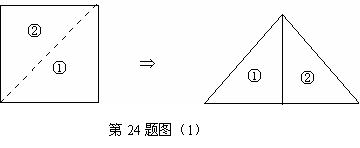
仿上面图示的方法,及韦达下列问题:
操作设计:
(1)如图(2),对直角三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积的矩形。
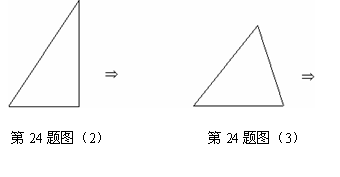
(2)如图(3)对于任意三角形,设计一种方案,将它分成若干块,再拼成一个原三角形等面积的矩形。
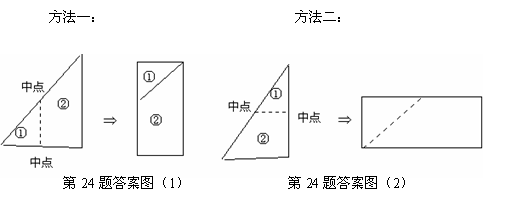 答案:(1)
答案:(1)
(2)略。
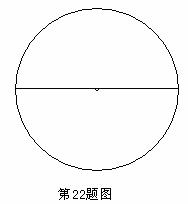
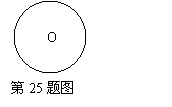 [25]如图,⊙O表示一圆形纸板,根据要求,需通过多次剪裁,把它剪成若干个扇形面,操作过程如下:第1次剪裁,将圆形纸板等分为4个扇形;第2次剪裁,将上次得到的扇形面中的一个再等分成4个扇形;以后按第2次剪裁的作法进行下去.
[25]如图,⊙O表示一圆形纸板,根据要求,需通过多次剪裁,把它剪成若干个扇形面,操作过程如下:第1次剪裁,将圆形纸板等分为4个扇形;第2次剪裁,将上次得到的扇形面中的一个再等分成4个扇形;以后按第2次剪裁的作法进行下去.
(1)请你在⊙O中,用尺规作出第2次剪裁后得到的7个扇形(保留痕迹,不写作法).
(2)请你通过操作和猜想,将第3、第4和第n次裁剪后所得扇形的总个数(S)填入下表.
|
等分圆及扇形面的次数(n) |
1 |
2 |
3 |
4 |
… |
n |
|
所得扇形的总个数(S) |
4 |
7 |
|
|
… |
|
(3)请你推断,能不能按上述操作过程,将原来的圆形纸板剪成33个扇形?为什么?
答案:(1)由图知六边形各内角相等.
(2) 七边形是正七边形.
(3)猜想:当边数是奇数时(或当边数是3,5,7,9,…时),各内角相等的圆内接多边形是正多边形.
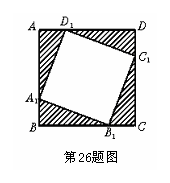 [26]如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1.试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原正方形面积的
[26]如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1.试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原正方形面积的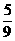 ,请说明理由(写出证明及计算过程).
,请说明理由(写出证明及计算过程).
答案:剪法是:当AA1=BB1=CC1=DD1=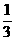 或
或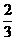 时,
时,
四边形A1B1C1D1为正方形,且S=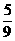 .
.
在正方形ABCD中,
AB=BC=CD=DA=1,
∠A=∠B=∠C=∠D=90°.
∵AA1=BB1=CC1=DD1,
∴A1B=B1C=C1D=D1A.
∴△D1AA1≌△A1BB1≌△B1CC1≌△C1DD1.
∴D1A1=A1B1=B1C1=C1D1,
∴∠AD1A1=∠BA1B1=∠CB1C1=∠DC1D1.
∴∠AA1D+∠BA1B1=90°,即∠D1A1B1=90°.
∴四边形A1B1C1D1为正方形.设AA1=x,
则AD1=1-x.
∵正方形A1B1C1D1的面积=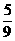 ,
,
∴S△AA1D1=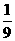
即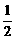 x(1-x)=
x(1-x)=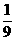 ,
,
整理得9x2-9x+2=0.
解得x1=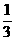 ,x2=
,x2=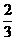 .
.
当AA1=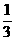 时,AD1=
时,AD1=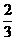 ,
,
当AA1=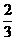 时,AD1=
时,AD1=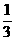 .
.
∴当AA1=BB1=CC1=DD1=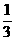 或
或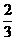 时,
时,
四边形A1B1C1D1仍为正方形且面积是原面积的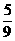 .
.
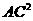 =100+1=101<
=100+1=101<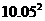

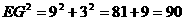 <
<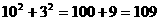 >
>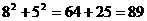 <
<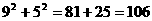 >
>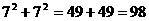 <
<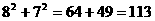 >
>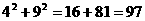 <
<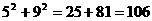 >
> [23]在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),张丰同学沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到菱形AECF(见方案二),请你通过计算,比较李颖同学和张丰同学的折法中,哪种菱形面积较大?
[23]在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),张丰同学沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到菱形AECF(见方案二),请你通过计算,比较李颖同学和张丰同学的折法中,哪种菱形面积较大?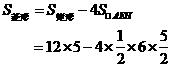

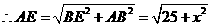
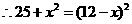
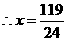
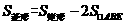
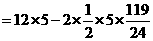
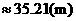

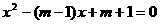 的两个实数根,试求出原矩形纸片的面积.
的两个实数根,试求出原矩形纸片的面积.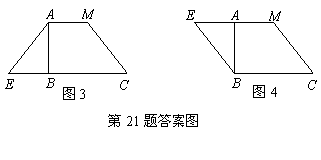
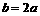
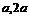 是方程
是方程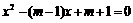 的两根
的两根

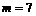 或
或
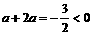 ,知
,知