21.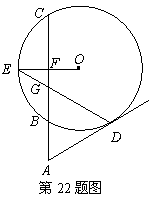 如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
⑴求证:AD是⊙O的切线;
⑵如果AB=2,AD=4,EG=2,求⊙O的半径.
|
∴OE⊥BC于F.
∴∠AGD+∠ODE=∠EGF+∠OED
=90°.……………………2分
连结OD.则OD=OE,
∴∠ODE=∠OED.……………………3分
∵∠AGD=∠ADG,
∴∠ADG+∠ODE=90°,即OD⊥AD.
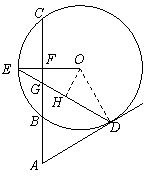 ∴AD是⊙O的切线.……………………5分
∴AD是⊙O的切线.……………………5分
⑵由AD=4,AB=2,AD2=AB·AC,得AC=8.……………………6分
∵AD=AG,∴BG=2,CG=4.
由EG=2,EG·GD=BG·CG,得DG=4.…………………………7分
∴AD=DG=GD,∴∠ADG=60°.
作OH⊥ED于H,则∠EOH=60°.…………………………………8分
在Rt△OEH中,EH=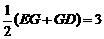 ,……………………………9分
,……………………………9分
∴OE=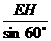 =
=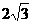 .
.
即⊙O的半径为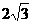 .………………………………………………10分
.………………………………………………10分
 (2)若CD=2,CB=
(2)若CD=2,CB= ,求EF的长;
,求EF的长;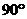 ,
,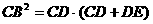 ,∵
,∵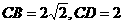 ,
,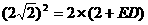 ,∴
,∴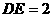 ,∴
,∴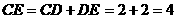 ,
,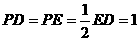 ,
,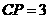 ,
,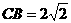 ,∴
,∴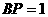 ,
,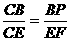 ,而
,而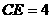 ,
,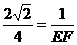 ,∴
,∴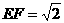
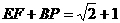 ,
,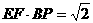
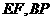 为根的方程是:
为根的方程是: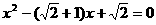
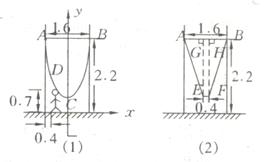
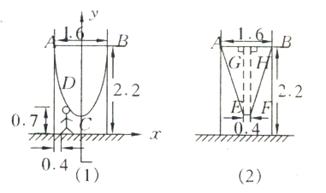 为供孩子们打秋千,把绳子剪断后,中间系上一块长为
为供孩子们打秋千,把绳子剪断后,中间系上一块长为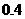 米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,(1)求绳子未剪断时最低点到地面的距离;(2)求剪断绳子系上木板时,木板到地面的距离。(供选用数据:
米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,(1)求绳子未剪断时最低点到地面的距离;(2)求剪断绳子系上木板时,木板到地面的距离。(供选用数据: ,
,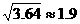 ,
,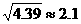 )
)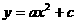
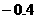 ,
,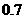 ),
),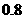 ,
,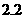 )
)
 ∴
∴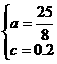 ,∴绳子最低点到地面的距离为
,∴绳子最低点到地面的距离为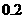 米。
米。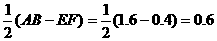
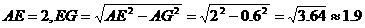
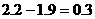 (米)
(米)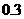 米。
米。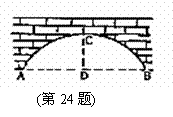 (10分)有一个拱桥是圆弧形,他的跨度为60
(10分)有一个拱桥是圆弧形,他的跨度为60 ,拱高为18
,拱高为18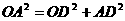 ,而OA =
,而OA = ,AD = 30,CD = 18
,AD = 30,CD = 18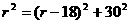
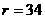
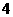 米时,水面所在弦的弦心距为:
米时,水面所在弦的弦心距为: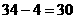 米,设水面所在的弦为
米,设水面所在的弦为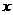 ,由勾股定理可知:
,由勾股定理可知: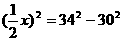 ,∴
,∴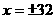 ,负值舍去,∴
,负值舍去,∴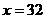
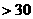
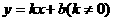 的图象与
的图象与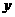 轴分别交于
轴分别交于 、
、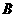 两点,且与反比例函数
两点,且与反比例函数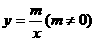 的图象在第一象限交于
的图象在第一象限交于 点,
点,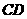 ⊥
⊥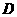 ,
,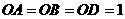 (1)求点
(1)求点
 y
y
 x
x ,0)、B(0,1)、D(1,0);
,0)、B(0,1)、D(1,0);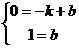
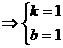
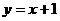 ,
,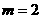 ,
,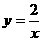 ,
,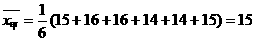 ,
,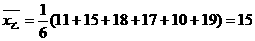
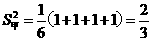 ,
,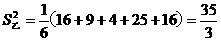 ,
,
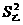 ,
, ),由于高度一致,平均数一致,所以方差为零,即
),由于高度一致,平均数一致,所以方差为零,即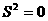 ,这样的石阶路走起来更舒适。
,这样的石阶路走起来更舒适。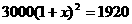
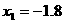 (不符题意,舍去),
(不符题意,舍去),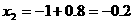
 。
。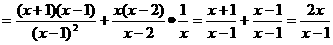
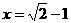 时,原式
时,原式