摘要：26．已知:如图.⊙O与⊙P相交于A.B两点.点 P在⊙O上.⊙O的弦AC切⊙P于点A.CP及其延长线交⊙P于D.E.过点 E作EF⊥CE交CB的延长线于F. (1)求证:BC是⊙P的切线, (2)若CD＝2.CB＝.求EF的长, (3)求以BP.EF为根的一元二次方程, 解:(1)∵点 P在⊙O上.连结PB. ∵CP为直径.∴∠CPB =. ∴PB⊥CB.∵B在⊙P上. ∴CB是⊙P的切线. (2)∵CB是⊙P的切线.∴.∵. ∴.∴.∴. ∴在⊙P中.. 在Rt⊿CPB中...∴. ∵EF⊥CE.∴∠FEC =∠CBP =.∠FCE =∠PCB.∴⊿FCE∽⊿PCB. ∴.而...∴.∴ (3)∵. ∴所求以为根的方程是:
网址：http://m.1010jiajiao.com/timu3_id_443090[举报]
与
相交于A、B两点，过A的直线交
21、已知：如图，⊙O1与⊙O2相交于A、B两点，过A的直线交⊙O1于C，交⊙O2于D，过B的直线交⊙O1于E，交⊙O2于F，且CD∥EF．
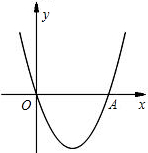已知：如图，二次函数y=x2+（2k-1）x+k+1的图象与x轴相交于O、A两点．（1）求这个二次函数的解析式；
（2）在这条抛物线的对称轴右边的图象上有一点B，使锐角△AOB的面积等于3．求点B的坐标；
（3）对于（2）中的点B，在抛物线上是否存在点P，使∠POB=90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由． 查看习题详情和答案>>
交⊙O于F，GF切⊙O于F且与CP交于G，CH切⊙O于C且与AB的延长线交于H，如果GP2=GD•GC，AD平分∠BAP并交HP于M．