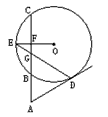
摘要:21.如图.割线ABC与⊙O相交于B.C两点.D为⊙O上一点.E为BC的中点.OE交BC于F.DE交AC于G.∠ADG=∠AGD. ⑴求证:AD是⊙O的切线, ⑵如果AB=2.AD=4.EG=2.求⊙O的半径. ⌒ ⑴证明:∵E为BC的中点. ∴OE⊥BC于F. ∴∠AGD+∠ODE=∠EGF+∠OED =90°.--------2分 连结OD.则OD=OE. ∴∠ODE=∠OED.--------3分 ∵∠AGD=∠ADG. ∴∠ADG+∠ODE=90°.即OD⊥AD. ∴AD是⊙O的切线.--------5分 ⑵由AD=4.AB=2.AD2=AB·AC.得AC=8.--------6分 ∵AD=AG.∴BG=2.CG=4. 由EG=2.EG·GD=BG·CG.得DG=4.----------7分 ∴AD=DG=GD.∴∠ADG=60°. 作OH⊥ED于H.则∠EOH=60°.-------------8分 在Rt△OEH中.EH=.-----------9分 ∴OE==. 即⊙O的半径为.------------------10分
网址:http://m.1010jiajiao.com/timu3_id_443085[举报]
 14、如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD,AB=2,AD=4,EG=2.
14、如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD,AB=2,AD=4,EG=2.求证:∠A=60°.
 如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.(1)求证:AD是⊙O的切线;
(2)如果AB=2,AD=4,EG=2,求⊙O的半径. 查看习题详情和答案>>
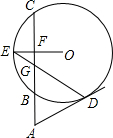 G=∠AGD.
G=∠AGD. 如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD,AB=2,AD=4,EG=2.
如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD,AB=2,AD=4,EG=2.