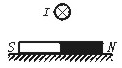1.如图所示，条形磁铁放在水平桌面上，在其正中间的上方固定一根长直导线，导线与磁铁垂直，给导线通以垂直纸面向里的电流，用F_N表示磁铁对桌面的压力，用F_μ表示桌面对磁铁的摩擦力，电线中通电后(与通电前相比较)( )

A.F_N减小，F_μ=0　　　　　　 B.F_N减小，F_μ≠0

C.F_N增大，F_μ=0　　　　　　 D.F_N增大，F_μ≠0

22.如图所示，在Ox轴上方有一个方向垂直纸面向里的匀强磁场，磁感应强度为B，在Ox轴下方有一个方向平行于Ox轴向右的匀强电场，场强为E，一个带电粒子的质量为m，电量为q，初速度为v₀，从a点垂直于磁场且水平地飞入磁场，然后运动到d点再垂直于Ox轴方向飞入电场中，最后经过c点(粒子的重力可忽略不计)，试问：(1)粒子自a点飞入，需经过多少时间到达c点？

(2)Oc之间的距离等于多少？

(3)粒子飞过c点的速度有多大？

《磁场》单元检测题

姓名：_______________

21.如图所示，AC为一竖直放置的圆弧形细管，圆弧半径为R，细管内径不计，OA、OC分别为水平和竖直半径，细管位于磁感强度为B的水平匀强磁场中。一质量为m的光滑带电小球，从A点由静止起下滑，到达C点时对管恰好无压力，则小球带 　　电荷，到达C点时的速率v_c=　 ，小球的电量q=　　　 。

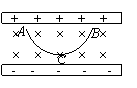20.设空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场，如图所示。已知一离子在电场力和洛仑兹力的作用下，从静止开始自A点沿曲线ACB运动，到达B点时速度为零。C点是运动的最低点，不计重力，以下说法中正确的是：(　　 )

A这离子必带正电荷

BA点和B点位于同一高度

C离子在C点时速度最大

D离子到达B点后，将沿原曲线返回A点。

3、带电粒子在复合场中的运动及其分析方法

(1)复合场

　　　 同时存在电场和磁场的区域，同时存在磁场和重力场的区域，同时存在电场、磁场和重力场的区域，都叫做复合场。

　　　 注意：电子、质子、a粒子、离子等微观粒子在复合场中运动时，一般都不计重力。但质量较大的质点(如带电尘粒)在复合场中运动时，不能忽略重力。

(2)带电粒子垂直进入E和B正交的复合场(速度选择器原理)

　　　 带电粒子受力特点：电场力与洛仑兹力方向相反(重力忽略)。

　　　 粒子匀速通过速度选择器的条件： qE=Bqv₀ ；即v₀=E/B；

　　　 若欲保证电场力与洛仑兹力方向始终相反，应将v₀、E、B三者中任意两个量的方向同时改变，但不能同时改变三个或任一个方向，否则将破坏速度选择功能。

　　　 当进入速度选择器的粒子的速度v₀¹E/B时，粒子将因偏移而不能通过速度选择器。设在电场方向偏转Dd后，粒子的速度为v。则当v>E/B时：粒子向f_洛方向偏移，电场力做负功，粒子动能减少，电势能增加。根据能量守恒定律有：mv₀²/2=qEDd+ mv²/2；则当v<E/B时：粒子向f_洛方向偏移，电场力做正功，粒子动能增加，电势能减少。根据能量守恒定律有：mv₀²/2+qEDd= mv²/2。

(3)正确分析带电粒子的受力及运动特征是解决问题的前提，灵活选用力学规律是解决问题的关键。

　　　 当带电粒子在复合场中所受合外力为零时，做匀速直线运动。一般可选用平衡条件列方程求解。

　　　 当带电粒子所受的重力与电场力等值反向，洛仑兹力提供向心力时，带电粒子在垂直于磁场的平面内做匀速圆周运动。一般可应用牛顿第二定律和平衡条件列方程联立求解。

　　　 当带电粒子所受的合外力是变力，且与初速度方向不在一条直线上时，粒子做非匀变速曲线运动，这时粒子的轨迹即不是圆弧，也不是抛物线。一般可选用动能定理或能量守恒定律列方程求解。

　　　 如果涉及到两个带电粒子的碰撞问题，还可根据动量守恒定律及其它方程求解。

　　　 19.如图所示的是一个互相垂直的匀强电场和匀强磁场，电场强度为E，磁感应强度为B，带电粒子重力不计，垂直电场和磁场方向射入场中，可能有Oa、Ob或OC三条轨迹，则下列说法中正确的是(　　 )

AOa可能是带正电荷粒子的轨迹，因为v>E/BBOb只能是速率等于E/B的带电粒子的轨迹，与粒子所带电荷性质无关

COc可能是带负电荷粒子的轨迹，因为v>E/BDOc可能是带正电荷粒子的轨迹，因为v>E/B。

18.如图所示为一个动量为P，电量为e的电子穿过宽度为d、磁感应强度为B的匀强磁场的情况，已知电子进入磁场时与磁场左侧的边缘垂直，则电子穿过磁场而产生的运动方向的偏转角a=?

17.如图所示，矩形匀强磁场区域的长为L、宽为L/2、磁感应强度为B，质量为m、电量为e的电子贴着矩形磁场的上方边界射入磁场，欲使该电子由下方边界穿出磁场。求：(1)电子速率v的取值范围(2)电子在磁场中运动时间t的变化范围。

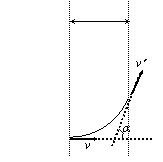
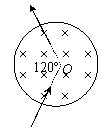16.如图所示的理想圆形磁场，半径为R，磁感强度为B，一质子(质量为m、电量为e)向着圆心方向射入磁场，离开磁场时方向与射入方向的夹角为120°，则质子通过磁场的时间t=？

2、确定轨道圆心和计算速度偏向角j、回旋角a和弦切角q的定量关系的方法。

在洛仑兹力作用下，一个做匀速圆周运动的粒子，不论沿顺时针方向还是逆时针方向，从A点运动到B点，均具有三个重要特点：1)轨道圆心(O)总是位于A、B两点洛仑兹力(f)作用线的交点上或AB弦的中垂线(OO¢)与任一个f作用线的交点上；

2)粒子的速度偏向角(j)等于回旋角(a)，并等于AB弦与切线的夹角(弦切角q)的2倍，即j=a=2q=wt；

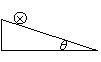15.在倾角为q的光滑斜面上置一通有电流I，长为L、质量为M的导体棒，如图所示。(1)欲使棒静止在斜面上，外加匀强磁场的磁感应强度B的最小值为　 ，方向应　 ；(2)欲使棒静止在斜面上且对斜面无压力，应加匀强磁场B的最小值为　 ，方向应是　　 。