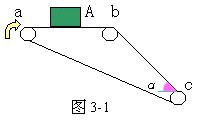
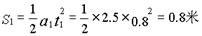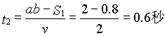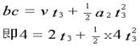0 137632 137640 137646 137650 137656 137658 137662 137668 137670 137676 137682 137686 137688 137692 137698 137700 137706 137710 137712 137716 137718 137722 137724 137726 137727 137728 137730 137731 137732 137734 137736 137740 137742 137746 137748 137752 137758 137760 137766 137770 137772 137776 137782 137788 137790 137796 137800 137802 137808 137812 137818 137826 447348
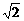 s D.(
s D.(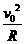 [1]
[1]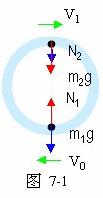
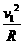 [3]
[3] 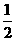 m2V12+m2g2R=
m2V12+m2g2R=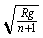 =
=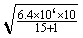 =2.0X103 m/s
=2.0X103 m/s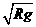 =7.9×103m/s,这就是第一宇宙速度,即环绕速度。
=7.9×103m/s,这就是第一宇宙速度,即环绕速度。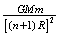 =
=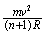 [1]
[1] 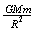 [2]
[2]