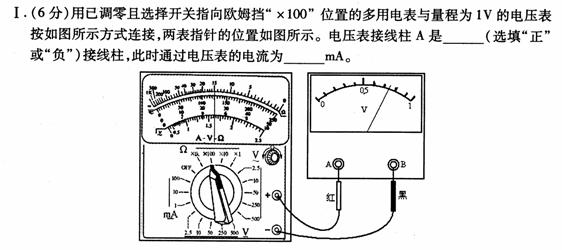
0 137222 137230 137236 137240 137246 137248 137252 137258 137260 137266 137272 137276 137278 137282 137288 137290 137296 137300 137302 137306 137308 137312 137314 137316 137317 137318 137320 137321 137322 137324 137326 137330 137332 137336 137338 137342 137348 137350 137356 137360 137362 137366 137372 137378 137380 137386 137390 137392 137398 137402 137408 137416 447348

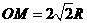 ,
① 2分
,
① 2分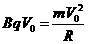 ② 1分
② 1分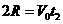 ③ 1分
③ 1分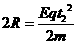 2分
由①②③④得:
2分
由①②③④得: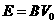 ⑤ 2分
⑤ 2分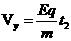 ⑥ 1分
⑥ 1分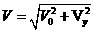 ⑦ 1分
⑦ 1分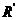 ,则再由牛顿第二定律得:
,则再由牛顿第二定律得:  ⑧ 1分
⑧ 1分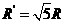 ⑨ 2分
⑨ 2分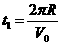 ⑩ 2分
⑩ 2分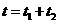 (11)1分
(11)1分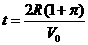
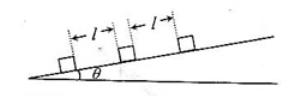 工人的推力;
工人的推力;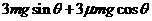 ;(2)
;(2)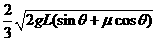 ;(3)
;(3)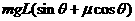 。
。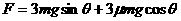
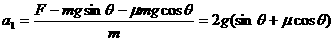 根据运动学公式或动能定理有
根据运动学公式或动能定理有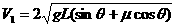 ,碰撞后的速度为V2根据动量守恒有
,碰撞后的速度为V2根据动量守恒有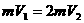 ,即碰撞后的速度为
,即碰撞后的速度为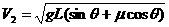 ,然后一起去碰撞第三个木箱,设碰撞前的速度为V3
,然后一起去碰撞第三个木箱,设碰撞前的速度为V3 ,根据运动学公式有
,根据运动学公式有 ,得
,得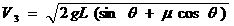 ,跟第三个木箱碰撞根据动量守恒有
,跟第三个木箱碰撞根据动量守恒有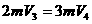 ,得
,得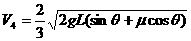 就是匀速的速度.
就是匀速的速度.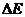 ,根据能量守恒有
,根据能量守恒有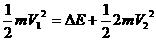 ,带入数据得
,带入数据得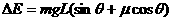 。
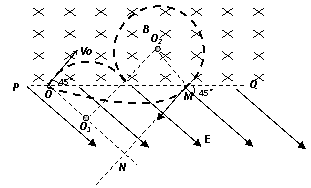
。 如图甲所示,Q1、Q2为两个固定点电荷,其中Q2带正电荷,它们连线的延长线上有a、23.(18分)如图所示,三个宽度均为d的区域I、Ⅱ和III,其中I、III内分别有方向垂于纸面向内和向外的匀强磁场(虚线为磁场边界面,并不表示障碍物),磁感应强度大小均为
如图甲所示,Q1、Q2为两个固定点电荷,其中Q2带正电荷,它们连线的延长线上有a、23.(18分)如图所示,三个宽度均为d的区域I、Ⅱ和III,其中I、III内分别有方向垂于纸面向内和向外的匀强磁场(虚线为磁场边界面,并不表示障碍物),磁感应强度大小均为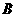 。设
。设 为过
为过 点垂直于
点垂直于 的直线,交
的直线,交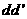 于
于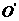 点,某种带负电的粒子从
点,某种带负电的粒子从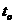 ;速度为V2时粒子在区域I内的运动时间为
;速度为V2时粒子在区域I内的运动时间为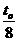 。求:
。求: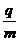 ;
;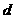 ;
;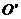 点的距离
点的距离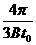 (2)
(2)
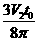 (3)
(3)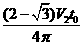
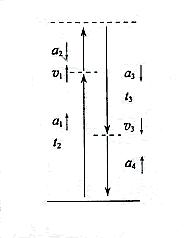
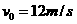 的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为
的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为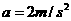 的加速度减速滑行。在车厢脱落
的加速度减速滑行。在车厢脱落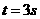 后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。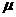 ;刹车前卡车牵引力的大小为
;刹车前卡车牵引力的大小为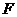 ,
,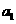 和
和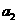 。重力加速度大小为g。由牛顿第二定律有
。重力加速度大小为g。由牛顿第二定律有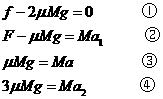
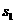 ,末速度为
,末速度为 ,根据运动学公式有
,根据运动学公式有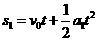 ⑤
⑤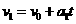 ⑥
⑥ ⑦
⑦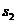 是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为
是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为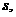 ,有
,有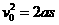 ⑧
⑧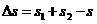 ⑨
⑨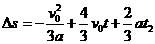 10
10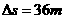 11
11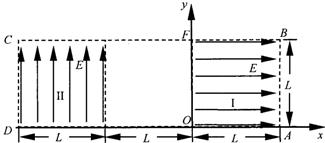 十三:电磁场偏转问题
十三:电磁场偏转问题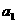
 匀加速运动
匀加速运动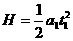
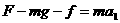
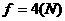
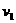 ,上升的高度为
,上升的高度为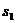
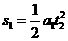
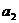 ,上升的高度为
,上升的高度为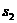
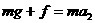
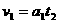

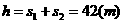
 ;恢复升力后加速度为
;恢复升力后加速度为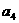 ,恢复升力时速度为
,恢复升力时速度为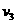
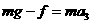
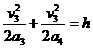
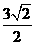 (s)(或2.1s)
(s)(或2.1s)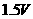 ,内阻约几欧姆
,内阻约几欧姆 、
、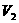 ,量程均为
,量程均为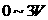 ,内阻约为3kΩ
,内阻约为3kΩ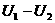 图像如图乙所示,图中直线斜率为k,与横轴的截距为a,则电源的电动势E= ▲
,内阻为r= ▲ (用k、a、R0表示)。
图像如图乙所示,图中直线斜率为k,与横轴的截距为a,则电源的电动势E= ▲
,内阻为r= ▲ (用k、a、R0表示)。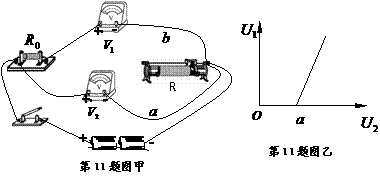

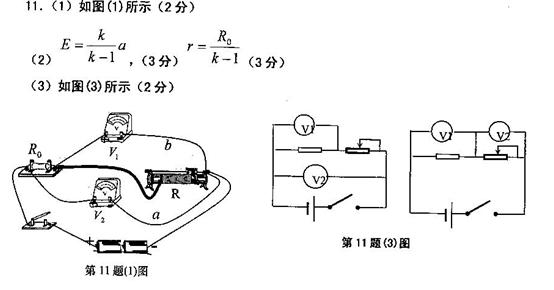
 某同学设计了一个探究平抛运动的家庭实验装置,如图所示。他的实验步骤如下:
某同学设计了一个探究平抛运动的家庭实验装置,如图所示。他的实验步骤如下: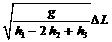 (2)
(2)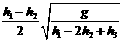
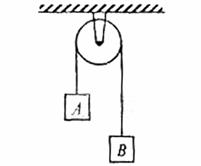 如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过定滑轮的软绳两端,已知m1>m2,现要利用此装置验证机械能守恒定律.
如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过定滑轮的软绳两端,已知m1>m2,现要利用此装置验证机械能守恒定律.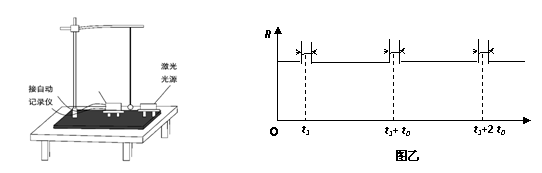

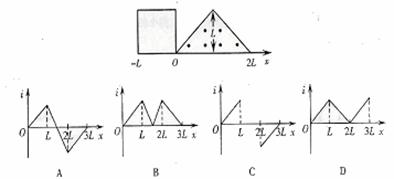
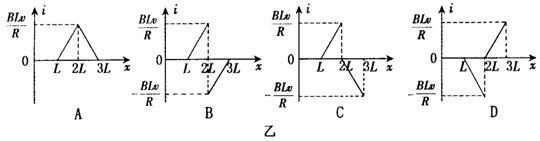
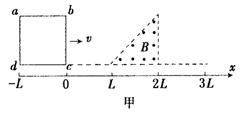 变化1:23.如图甲所示,有一个等腰直角三角形的匀强磁场区域,其直角边长为L,磁场方向垂直纸面向外,磁感应强度大小为B。一边长为L总电阻为R的正方形导线框abcd,从图示位置开始沿x轴正方向以速度v匀速穿过磁场区域。取沿a→b→c→d→a的感应电流为正,则图乙中表示线框中电流i随bC边的位置坐标x变化的图象正确的是 C
变化1:23.如图甲所示,有一个等腰直角三角形的匀强磁场区域,其直角边长为L,磁场方向垂直纸面向外,磁感应强度大小为B。一边长为L总电阻为R的正方形导线框abcd,从图示位置开始沿x轴正方向以速度v匀速穿过磁场区域。取沿a→b→c→d→a的感应电流为正,则图乙中表示线框中电流i随bC边的位置坐标x变化的图象正确的是 C