0 137199 137207 137213 137217 137223 137225 137229 137235 137237 137243 137249 137253 137255 137259 137265 137267 137273 137277 137279 137283 137285 137289 137291 137293 137294 137295 137297 137298 137299 137301 137303 137307 137309 137313 137315 137319 137325 137327 137333 137337 137339 137343 137349 137355 137357 137363 137367 137369 137375 137379 137385 137393 447348
 (2)解:①v=
(2)解:①v= =
= ×108m/s……………(2分)
×108m/s……………(2分) m……………………………………………………………………(1分)
m……………………………………………………………………(1分)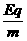 =2
=2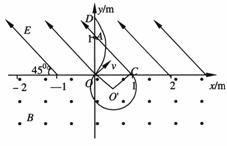 时间t=
时间t= =10-6s…………………………………………………………………(2分)
=10-6s…………………………………………………………………(2分) ……………………………(2分)
……………………………(2分) =
= m………………………………………………………………………(1分)
m………………………………………………………………………(1分)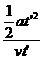 …………………………………………………………………………(2分)
…………………………………………………………………………(2分)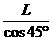 =8m…………………………………………………………………………(1分)
=8m…………………………………………………………………………(1分) =μg=5m/s2 …………………………………………………………………(1分)
=μg=5m/s2 …………………………………………………………………(1分) =3m/s2
…………………………………………………………………(1分)
=3m/s2
…………………………………………………………………(1分) t1 ………………………………………………………………………(1分)
t1 ………………………………………………………………………(1分) t1……………………………………………………………………………………(1分)
t1……………………………………………………………………………………(1分)
 t1=4m………………………………………………………………………(1分)
t1=4m………………………………………………………………………(1分) gt22…………………………………………………………………………………(1分)
gt22…………………………………………………………………………………(1分)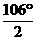 )=
)=  ………………………………………………………………………………(1分)
………………………………………………………………………………(1分)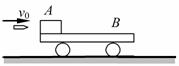 ①物体A的最大速度vA;
①物体A的最大速度vA;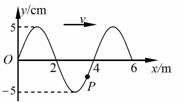 (1)一列正弦机械波在某一时刻的波形曲线如图所示,已
(1)一列正弦机械波在某一时刻的波形曲线如图所示,已 (2)如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,
(2)如图所示,一个横截面为直角三角形的三棱镜,∠A=30°, (18分)在如图所示的直角坐标中,x轴的上方存在与x轴正方向成45°角斜向右下方的匀强电场,场强的大小为E=
(18分)在如图所示的直角坐标中,x轴的上方存在与x轴正方向成45°角斜向右下方的匀强电场,场强的大小为E= =2×108C/㎏的正点电荷从坐标为(0,1)的A点处由静止释放。电荷所受的重力忽略不计。求:
=2×108C/㎏的正点电荷从坐标为(0,1)的A点处由静止释放。电荷所受的重力忽略不计。求:
 …………1分
…………1分 …………1分
…………1分 球的速度大小为
球的速度大小为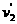 ,根据动量定恒定律的
,根据动量定恒定律的 …………2分
…………2分 …………2分
…………2分 …………2分
…………2分 ,则
,则 ………………………………(3分)
………………………………(3分)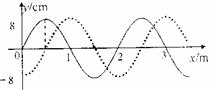 满足
满足 ,即
,即 ……(3分)
……(3分)