3．2古典概型（1）
[教学目标]
一、问题情境：将扑克牌（52张）反扣在桌上，先从中任意抽取一张，那么抽到的牌为红心的概率有多大？
问题分析：把“抽到红心”记为事件
，那么事件相当于“抽到红心
”这13中情况，而同样抽到其他牌的共有
种情况；由于是任意抽取的，可以认为这
中情况的可能性是相等的。所以，当出现红心是“抽到红心１”，“抽到红心２”，…，“抽到红心”这13中情形之一时，事件就发生，于是
；
说明：以上每个结果称为一个基本事件，每个结果出现的可能性是相同的，故又称等可能的基本事件
二、建构数学
1．基本事件：在一次试验中可能出现的每一个基本结果称为基本事件；
2．等可能基本事件：若在一次试验中，每个基本事件发生的可能性都相同，则称这些基本事件为等可能基本事件；
3．古典概型：满足以下两个条件的随机试验的概率模型称为古典概型
①所有的基本事件只有有限个；
②每个基本事件的发生都是等可能的；
4．古典概型的概率：
如果一次试验的等可能基本事件共有
个，那么每一个等可能基本事件发生的概率都是
，如果某个事件
包含了其中
个等可能基本事件，那么事件发生的概率为
．
例1、把一个骰子抛一次，设正面出现的点数为x
（1） 列出x的所有可能的取值情况
（2） 下列事件由哪些基本事件构成
① x的取值为2的倍数
② x的取值大于3
③ x的取值不超过2
④ x的取值为质素
（3） 判断满足上述条件的随机试验的概率模型是否为古典概型，并求其概率
解 ：（1）1，2，3，4，5，6
（2）①2，4，6
②4，5，6
③1，2
④2，3，5
（3）都是，
,,
例2、一个口袋内装有大小相同的5只球，其中3只白球,２只黑球,从中一次摸出两个球，(1)共有多少个基本事件？(2)摸出的两个都是白球的概率是多少？
分析：可用枚举法找出所有的等可能基本事件．
解：(1)分别记白球为1，2，3号，黑球4，5号，从中摸出2只球，有如下基本事件（摸到1,2号球用（1，2）表示）：
，
因此，共有10个基本事件．
（2）上述10个基本事件法上的可能性是相同的，且只有3个基本事件是摸到两个白球（记为事件A），即（1，2）（1，3）（2，3），故
∴共有10个基本事件，摸到两个白球的概率为
；
例3．豌豆的高矮性状的遗传由其一对基因决定，其中决定高的基因记为
，决定矮的基因记为
，则杂交所得第一子代的一对基因为
，若第二子代的
基因的遗传是等可能的，求第二子代为高茎的概率（只要有基因则其就是高茎，只有两个基因全是时，才显现矮茎）．
分析：由于第二子代的基因的遗传是等可能的，可以将各种可能的遗传情形都枚举出来．
解：Dd与Dd的搭配方式共有４中：
，其中只有第四种表现为矮茎，故第二子代为高茎的概率为
答：第二子代为高茎的概率为0.75．
思考1：第三代高茎的概率呢？
第一步：第二代基因分解:
第二步：非己的自由组合：
DD,Dd ,DD,Dd,DD,Dd,Dd,DD,Dd,DD,Dd,Dd,Dd,DD,Dd,Dd,Dd,dD,dd,dd,dd,dd,dd,Dd,Dd共24个，其中高茎有19个，概率19/24
思考2：古典概型解题步骤是什么？
S1:判断是否是等可能事件，并用字母表示事件；
S2:求出基本事件总数和事件所包含的结果数(常用列举法)
S3:用公式求出概率
S4:应用问题写答
[课堂练习]教材P97---练习题
[小结] 1．古典概型、等可能事件的概念；
2．古典概型求解??枚举法（枚举要按一定的规律）；
[课外作业]教材P97---98习题1~10
补充习题：
1、统计170名新生女婴的体重，得到如下频率分布表
分组编号
1
2
3
4
5
6
7
组距（g）
[1700，1900）
[1900，2100）
[2100，2300）
[2300，2500）
[2500，2700）
[2700，2900）
[2900，3100）
组频数
1
1
3
5
13
22
28
分组编号
8
9
10
11
12
13
组距（g）
[3100，3300）
[3300，3500）
[3500，3700）
[3700，3900）
[3900，4100）
[4100，4300）
组频数
39
28
20
7
2
1
从这170名新生女婴中任选一名，体重不小于
2、先后抛掷3枚均匀的一分、二分、五分硬币
（1）一共可能出现多少种不同结果？
（2）出现“2枚正面、1枚反面”的概率是多少？
（3）改为同时抛3枚相同的一分硬币结果还相同吗？
3、从两双不同的鞋子中随机拿出2只，求恰好配对的概率？
解答：1、0.176；
2、（1）8种（2）
（3）相同；
3、共有左1左2、左1右1、左1右2、左2右1、左2右2、右1右2六种取法，故恰好穿对的概率为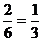
3.2 古典概型（2）
[教学目标]
[教学重点]古典概型的特征和用枚举法解决古典概型的概率问题．
[教学难点]理解古典概型的两个重要特征
[教学过程]
S1:判断是否是等可能事件，并用字母表示事件；
一、复习：解答等可能事件概率问题的方法步骤是什么？
S2:求出基本事件总数和事件所包含的结果数(常用列举法)
S3:用公式求出概率
S4:应用问题写答
二、例题与练习：
例1．将一颗骰子先后抛掷两次，观察向上的点数，问：
（1）共有多少种不同的结果？
（2）两数的和是3的倍数的结果有多少种？
（3）两数和是3的倍数的概率是多少？
解：（１）将骰子抛掷１次，它出现的点数有1,2,3,4,5,6这6中结果。
先后抛掷两次骰子，第一次骰子向上的点数有6种结果，第2次又都有6种可能的结果，于是一共有6×6=36种不同的结果；
(2)第1次抛掷，向上的点数为1,2,3,4,5,6,这6个数中的某一个，第2次抛掷时都可以有两种结果，使向上的点数和为3的倍数（例如：第一次向上的点数为4，则当第2次向上的点数为2或5时，两次的点数的和都为3的倍数），于是共有6×2=12种不同的结果．
(3)记“向上点数和为3的倍数”为事件A，则事件A的结果有12种，因为抛两次得到的36中结果是等可能出现的，所以所求的概率为
答：先后抛掷2次，共有36种不同的结果；点数的和是3的倍数的结果有12种；点数和是3的倍数的概率为
；
说明：也可以利用图表来数基本事件的个数：
练习：向上点数和为4的倍数的概率是多少？（第一次+第二次：1+3，2+2,2+6,3+1,3+5,4+4,5+3,6+2共8种情况，概率8/36=2/9）
例2． 用不同的颜色给右图中的3个矩形随机的涂色，每个矩形只涂一种颜色，求
(1)3个矩形颜色都相同的概率；
(2)3个矩形颜色都不同的概率．
分析：本题中基本事件比较多，为了更清楚地枚举出所有的基本事件，可以画图枚举如下：（树形图）
解：基本事件共有27个；
(1)记事件A＝“3个矩形涂同一种颜色”，由上图可以知道事件包含的基本事件有1×3=3个，故
(2)记事件B＝“3个矩形颜色都不同”，由上图可以知道事件B包含的基本事件有
个，故
答：3个矩形颜色都相同的概率为
；3个矩形颜色都不同的概率为
．
说明：这种列举的方法称树图列举法
例3．一个各面都涂有色彩的正方体，被锯成
个同样大小的小正方体，将这些正方体混合后，从中任取一个小正方体，求：⑴有一面涂有色彩的概率；⑵有两面涂有色彩的概率；⑶有三面涂有色彩的概率.
解：在1000个小正方体中，一面图有色彩的有82×6个，两面图有色彩的有8×12个，三面图有色彩的有8个，∴⑴一面图有色彩的概率为
；
⑵两面涂有色彩的概率为
；
⑶有三面涂有色彩的概率
.
答：⑴一面图有色彩的概率0.384；⑵两面涂有色彩的概率为0.096；⑶有三面涂有色彩的概率0.008.
练习：一个口袋内装有大小相等的一个白球和3个黑球，从中摸出2个球
（1）共有多少种不同的结果；（2）摸出2个黑球的概率是多少
解：（1）6种（2）
补充习题：
四、课外作业：教材P98―11~14
1、同时抛掷两个骰子，计算：
①向上的点数相同的概率； ②向上的点数之积为偶数的概率．
2、据调查，10000名驾驶员在开车时约有5000名系安全带，如果从中随意的抽查一名驾驶员有无系安全带的情况，系安全带的概率是 （ ）
3、在20瓶饮料中，有两瓶是过了保质期的，从中任取１瓶，恰为过保质期的概率为（ ）
4、将编号为1，2，3，4的贺卡随意地送给编号为1、2、3、4的四位老师，每位老师得到一张贺卡，记编号与贺卡编号相同的老师个数为m,求(1)m=1的概率；(2)m=0的概率
解答：1、（1）
（2）
；
2、C;
3、B
4、解：不妨将教师按1、2、3、4排好队不动，只要将卡片进行顺序交换，这样，总体含有的基本事件与1、2、3、4能组成的四位数等效，其中1为首位（从左到右数）如图
有6个，同理2、3、4占首位的也有6个，共计6×4=24个
（1）只有一个在对应位置上，可以是1、2、3、4中任何一个，比如只有1在首位，其余数不在自己位置上：这样2不在第二位，只能在第三或第四位置上，2位置确定了之后，3、4位置因不能在自己位置上，也就确定，这样只有1在自己首位上有两种情况；同理，只有2、3、4在自己位置上也各有两种情况。共有8种情况。P(m=1)=8/24=1/3