2009年北京市朝阳区初中毕业考试
数学试卷
第Ⅰ卷(选择题32分)
一、选择题(共8道小题,每小题4分,共32分)
1.5 的相反数是( )
A. 5 B.-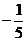 D.-
D.-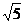
2.第十一届全国人大会议的政府工作报中指出,2009年全国教育支出预算约为10 946亿元,数字10 946用科学记数法表示为( )
A.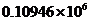 B.
B.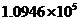 C.
C.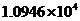 D.
D.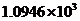
3.如下图,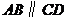 ,直线BC分别交AB、CD于点B、C,若∠1=50°,则∠2的度数为( )
,直线BC分别交AB、CD于点B、C,若∠1=50°,则∠2的度数为( )

A.40° B.50° C.120° D.130°
4.下列运算中,正确的是( )
A.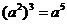 B.
B.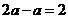 C.
C.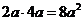 D.
D.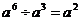
5.图中几何体的左视图是( )
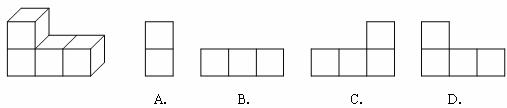
6.已知△ABC∽△DEF,且对应边AB:DE=2:1,那么△ABC与DEF的面积比为( )
A.1:1 B. 2:
7.一个袋子中装有1个红色球和3个黄色球,这些球除颜色外,形状、大小、质地等完全相同,在看不到球的条件下,随机地从这个袋子中摸出一个球,摸到红色球的概率为( )
A.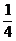 B.
B.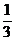 C.
C.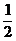 D.
D.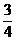
8.如下图,在菱形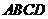 的对角线AC和BD相交于点O,AC=8,BD=6,将
的对角线AC和BD相交于点O,AC=8,BD=6,将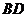 沿
沿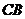 的方向平移,使点
的方向平移,使点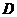 与点
与点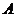 重合,这时点
重合,这时点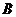 与
与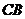 延长线上的点
延长线上的点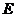 重合,则梯形
重合,则梯形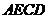 的面积等于(
)
的面积等于(
)
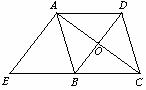
A.36 B.
第Ⅱ卷 (共68分)
二、填空题 (共5道小题,每小题4分,共20分)
9.在函数y =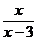 中,自变量x的取值范围是
.
中,自变量x的取值范围是
.
10.分解因式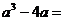 .
.
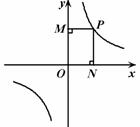
11.反比例函数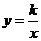 的图象如下图所示,点P是该函数图象上一点,PN垂直
的图象如下图所示,点P是该函数图象上一点,PN垂直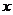 轴于点N,PM垂直y轴于点M, 如果矩形OMPN的面积为2,则
轴于点N,PM垂直y轴于点M, 如果矩形OMPN的面积为2,则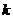 值为 .
值为 .
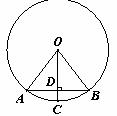
12. 如图,在⊙O中,弦AB=6,⊙O的半径长为5,OC⊥AB于点D,交⊙O于点C,则CD= .
13.如果关于x的一元二次方程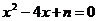 有两个相等的实数根,那么实数n的取值范围是 .
有两个相等的实数根,那么实数n的取值范围是 .
三.解答题 (共9道小题,14题―20题每小题5分,21题6分,22题7分,共48 分)
14.(本小题5分)
计算:?-2?+3sin30°-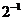 -(
-(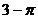 )0 .
)0 .
15.(本小题5分)
解不等式3(5+3x)≤5x-1,并把它的解集在下面的数轴上表示出来.
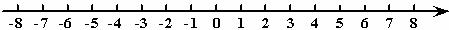
16.(本小题5分)
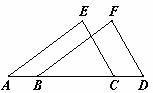
已知:如图,点A、B、C、D在同一直线上,且AB=CD,AE∥BF,AE=BF.
求证:∠E=∠F.
17. (本小题5分)
计算: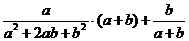 .
.
18.(本小题5分)
某中学为了解九年级300名学生的理化实验操作水平,从这300名学生中随机抽取30名学生进行测试,测试成绩5分以下(含5分)为不合格, 6分至9分(含6分和9分)为良好,10分为优秀. 下面是这30名学生的测试成绩表和相应的扇形统计图:
成绩
3
4
5
6
7
8
9
10
人数
2
4
6
a
7
2
2
b
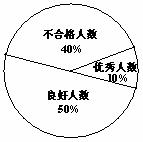
(1)求出测试成绩表中a和b的值;
(2)求出这30名学生测试成绩的平均数和众数;
(3)请估计该中学九年级300名学生中成绩为优秀的有多少人?
19. (本小题5分)
如下图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,BC=1,AC=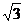 .
.
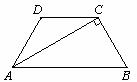
(1)求∠B的度数;
(2)求梯形ABCD的周长.
20.(本小题5分)
已知:如下图,△ABC中,AB=AC=5,BC=6,以AB为直径作⊙O交AC于点D,交BC于点E,EF⊥AC于F交AB的延长线于G.
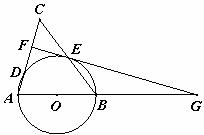
(1)求证:FG是⊙O的切线;
(2)求AD的长.
21.(本小题6分)
如下图,已知二次函数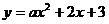 的图象与x轴交于点A、点B,与y轴交于点C,其顶点为D,tan∠OBC=1,
的图象与x轴交于点A、点B,与y轴交于点C,其顶点为D,tan∠OBC=1,
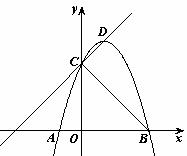
(1)求点B的坐标;
(2)求a的值和二次函数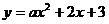 的顶点坐标;
的顶点坐标;
(3)求直线DC的解析式;
(4)在该二次函数的图象上是否存在点P(点P与点B、C不重合),使得ΔPBC是以BC为一条直角边的直角三角形?若存在,求出点P的坐标,若不存在,请你说明理由.
22.(本小题7分)
有一根直尺的短边长2┩,长边长10┩,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm.
如图①,将直尺的短边DE与直角三角形纸板的斜边AB重合,且点D与点A重合; 将直尺沿AB方向平移(如图②),设平移的长度为xcm( 0 ≤ x ≤ 10 ),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为Scm2.
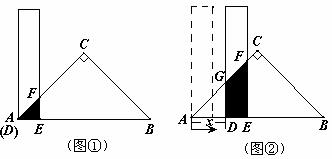
(1)当x=0时(如图①),S=_____________;.
(2)当0<x ≤ 4时(如图②),求S关于x的函数关系式;
(3)当4<x<6时,求S关于x的函数关系式;
(4)直接写出S的最大值.