太 原 五 中
2006―2007学年度第二学期月考试题(5月)
高 三 数 学(理)
一、选择题(每小题只有一个正确选项,每题5分)
1. 设全集U=R,M={x | x>2},N={x | <2},那么下列关系中正确的是
A.M=N B.N Í M C.M Í N D.M∩N = F
2. 设复数z满足(2+i)z=1-i,那么复数z等于
A.1-i B.1+i C.+i D.-i
3. 若△ABC的内角满足sinA+cosA>0,tanA-sinA<0,则角A的取值范围是
A.(0, ) B.(,) C.(,) D.(,p )
4. 已知等差数列{a n}的公差为2,若a1,a3,a4成等比数列,则a2的值为
A.-4 B.-6 C.-8 D.-10
5. 不等式组 有解,则实数a的取值范围是
A.(-1,3) B.(-3,1)C.(-¥,1)∪(3,+¥) D.(-∞,-3)∪(1,+¥)
6.
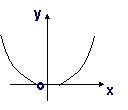
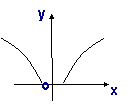
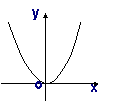
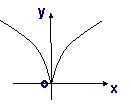 函数
函数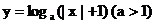 的大致图像是
的大致图像是
A B C D
7. 函数f(x)与g(x)=()x的图像关于直线y=x对称,则f(4x- x2)的单调递增区间为
A.(-¥,2) B.(0,2) C.(2,4) D.(2,+¥)
8. 如图,在下列六个图中,每个小四边形皆为全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的是
 |
|||||||||||
 |
 |
||||||||||
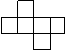 |
|||||||||||
 |
|||||||||||
 |
|||||||||||
① ② ③ ④ ⑤ ⑥
A.① ② ④ B.① ③ ⑤ ⑥ C.② ⑤ ⑥ D.① ③ ⑥
9.
某批袋装食品的质量服从正态分布N (500,4) (单位:g),任选购一袋此种食品,其质量在
A.2j (1)-1 B.1-j (1) C.j (1) D.j (1)-
10. 将函数y=sinx-cosx的图像向右平移了j 个单位,所得图像关于y轴对称,则j 的最小正值是
A. B. C. D.
11. 已知f (x)是R上的偶函数,对x Î R都有f (x+6)=f (x)+f (3)成立,则f(2007)=
A.2007 B.
12. 已知椭圆 ,则其内接三角形面积的最大值为
A.6 B.
二、填空题(每小题4分)
13.
在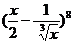 的展开式中常数项是________.
的展开式中常数项是________.
14. 实数x,y满足方程 x2+y2=6x-4y-9,则2x-3y的最大值与最小值的和等于 。
15. 若∆ABC内切圆半径为r,三边长为a、b、c,则∆ABC的面积S=r (a+b+c). 若四面体内切球半径为R,四个面的面积为S1、S2 、S3 、S4,则四面体的体积V=
16. 某商场开展促销抽奖活动,摇出的中奖号码是8,2,5,3,7,1,参加抽奖的每位顾客从0~9这10个号码中任意抽出六个组成一组,若顾客抽出的六个号码中至少有5个与摇出的号码相同(不计顺序)即可得奖,则中奖的概率是________.
太 原 五 中
2006―2007学年度第二学期月考试题(5月)
高三数学答卷纸(理)
题 号
一
二
三
总 分
17
18
19
20
21
22
得 分
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题(每小题4分)
13.常数项是________. 14.最大值与最小值的和等于 。
15.四面体的体积V= 16.中奖的概率是 .
三、解答题
17. (12分)已知函数f (x)=2cos2x+sin2x+a (aÎ R).
(Ⅰ)若x∈R,求f(x)的单调递增区间;
(Ⅱ)若x∈[0,]时,f(x)的最大值为4,求a的值,并指出这时x的值.
18.
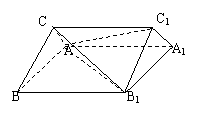 (12分)如图.已知斜三棱柱ABC- A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为,且侧面ABB1 A1垂直于底面ABC.
(12分)如图.已知斜三棱柱ABC- A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为,且侧面ABB1 A1垂直于底面ABC.
(Ⅰ)求证:点B1在平面ABC上的射影为AB的中点;
(Ⅱ)求二面角C-AB1-A1的大小;
(Ⅲ)求直线B1C与C1A所成的角.
19. (14分)某人投篮命中率为0.7,且各次投篮的结果互不影响。
(Ⅰ)若连续投中两次就停止,求最多投篮三次就停止的概率;
(Ⅱ)若连续投篮4次,记投中的次数与没投中的次数之差为ξ。
(1)写出ξ的分布列;(2)求ξ的期望与方差。
20. (12分)设f (x)是定义在R上的偶函数,其图象关于x=1对称,对任意x1,x2 Î[0,],都有f (x1+x2)=f (x1) f (x2),且f (1)=a>0.
(Ⅰ)求f ()及f ();
(Ⅱ)证明f (x)是周期函数;
(Ⅲ)记a n=f (2n+),求 (lna n)。
21.
(本题12分)已知椭圆C的方程为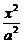 +
+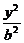 =1(a>b>0),双曲线
=1(a>b>0),双曲线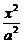 -
-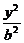 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B.(如图)
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B.(如图)
 (Ⅰ)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(Ⅰ)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(Ⅱ)当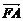 =λ
=λ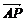 时,求λ的最大值.
时,求λ的最大值.
22. (12分)已知函数f (x)=x2+lnx..
(Ⅰ)求函数f (x)在区间[1,e]上的最大值、最小值;
(Ⅱ)求证:在区间[1,+¥]上,函数f (x)的图象在函数g (x)=x3的下方;
(Ⅲ)设h (x)=f ′ (x),求证:[h (x)] n+2≥h (x n)+2 n.
太 原 五 中
2006―2007学年度第二学期月考试题(5月)
高三数学答案(理)
1
2
3
4
5
6
7
8
9
10
11
12
C
D
C
B
A
C
C
D
A
C
D
B
二、填空题(每小题4分)
13.7 14.24 15.R(S1+S2+S3+S4) 16.
17.解:(1)f (x)=sin2x+cos2x+1+a=2sin(2x+)+1+a.…………………………3分
解不等式2kp-≤2x+≤2kp+.
得kp-≤x≤kp+ (k ÎZ)
∴ f (x)的单调增区间为[kp-,kp+] (k ÎZ). ……………………………6分
(2)∵ x Î [0,], ∴ ≤2x+≤. ……………………………8分
∴ 当2x+=,即x=时,f (x)max=3+a. ……………………………10分
 ∵ 3+a=4,∴ a=1,此时x=.
……………………………12分
∵ 3+a=4,∴ a=1,此时x=.
……………………………12分
18.解析:(1)如图,在平面ABB1A1内,过B1作B1D⊥AB于D,
∵ 侧面ABB1A1⊥平面ABC,
∴ B1D⊥平面ABC,∠B1BA是B1B与平面ABC所成的角,
∴ ∠B1BA=60°. ……………………………2分
∵ 四边形AB B1A1是菱形,
∴ △AB B1为正三角形,
∴ D是AB的中点,即B1在平面ABC上的射影为AB的中点.…………………4分
(2)连结CD,∵ △ABC为正三角形,
又∵ 平面ABB1A1⊥平面ABC,平面ABB1A1∩平面ABC=AB,
∴ CD⊥平面ABB1A1,在平面ABB1A1内,过D作DE⊥A1B于E,
连结CE,则CE⊥A1B,
∴ ∠CED为二面角C- AB1-B的平面角. ……………………………6分
在Rt△CED中,CD=2sin60° =,
连结A1B于O,则BO=,DE=BO=,
∴ tan∠CED==2.
∴ 所求二面角C-AB1-A1的大小为p-arctan2. ……………………………8分
(3)解:连结BC1,
∵ BB1CC1是菱形 ∴ BC1⊥B1C.
∴ CD⊥平面ABB1A1,B1D⊥AB, ∴ B1C⊥AB,
∴ B1C⊥平面ABC1, ∴ B1C⊥C1A. ……………………………12分
19.解:(Ⅰ) 投篮两次就停止的概率为 0.7×0.7=0.49,
投篮两次停止的概率为 0.3×0.7×0.7=0.147,
∴ 最多投篮三次就停止的概率为P=0.49+0.147=0.637. ……………………4分
(Ⅱ)解:(1)记连续投篮4次投中的次数为η,则没投中的次数为4-η,
∴ ξ=η-(4-η)=2η-4.
∴ ξ的可能取值为-4,-2,0,2,4. ……………………6分
P(ξ=-4)=0.34=0.0081, P(ξ=-2)=×0.7×0.33=0.0756,
P(ξ=0)=×0.72×0.32=0.2646, P(ξ=2)=×0.73×0.3=0.4116,
P(ξ=4)=×0.74=0.2401.
ξ
-4
-2
0
2
4
P
0.0081
0.0756
0.2646
0.4116
0.2401
ξ的分布列为
………………………10分
(2)∵η~B(4,0.7), ∴ Eη=4×0.7=2.8,Dη=4×0.7×0.3=0.84。
∴ Eξ=E(2η-4)=2Eη-4=5.6-4=1.6, ………………………12分
Dξ=4 Dη=3.36. ………………………14分
20.解:(Ⅰ)令x1=x2=,得f(1)=f()2,∴ f()=。 …………………2分
令x1=x2=,得f()=f()2,∴ f()=. …………………4分
(Ⅱ)x=1对称有f(2-x)=f(x),又偶函数,∴ f(-x)=f(x),…………………5分
于是有f(2-x)=f(-x),对于任意x都成立,
用-x换x得f(2+x)=f(x)总成立,
∴函数是周期函数,T=2是它的一个周期。 …………………7分
(Ⅲ)∵f(x)的周期是2,∴an=f(2n+)=f(), ……………………8分
而f()=f(n×)=f()f[(n-1)×]=f()?f()?…?f()=f n()
故an=[f()] ,即 an=a . ……………………10分
因此, (ln an)= (ln a )= (ln a)=0。 ……………………12分
21.解:(1)∵双曲线的渐近线为y=±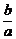 x,两渐近线夹角为60°,又
x,两渐近线夹角为60°,又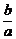 <1,
<1,
∴∠POx=30°,即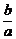 =tan30°=
=tan30°= . ∴a=
. ∴a=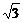 b.
…………………3分
b.
…………………3分
又a2+b2=4, ∴a2=3,b2=1.
故椭圆C的方程为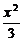 +y2=1.
……………………5分
+y2=1.
……………………5分
(2)由已知l:y=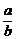 (x-c),与y=
(x-c),与y=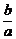 x解得P(
x解得P(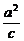 ,
,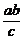 ), …………………7分
), …………………7分
由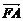 =λ
=λ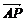 得A(
得A(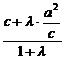 ,
,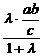 )
………………………9分
)
………………………9分
将A点坐标代入椭圆方程得
(c2+λa2)2+λ2a4=(1+λ)2a2c2
∴(e2+λ)2+λ2=e2(1+λ)2 ……………………10分
∴λ2=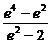 =-[(2-e2)+
=-[(2-e2)+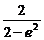 ]+3≤3-2
]+3≤3-2
∴λ的最大值为 -1.
…………………12分
-1.
…………………12分
23. 解:(Ⅰ)∵f ′(x)在区间[1,e]上是增函数,
∴ 最大值是+1,最小值是. ………………2分
(Ⅱ)设F(x)=x2+lnx-x3,
则F'(x)=x+-2x2=. ……………………4分
∵x>1,∴F'(x)<0,所以函数F(x)在区间(1,+¥)上单调递减。…………………5分
又 F(1)=-<0,∴ 在区间(1,+¥)上,F(x)<0,
即 x2+lnx<x3.
∴函数f (x)的图象在函数g (x)=x3的下方. ……………………7分
(Ⅲ)当n=1时,不等式成立。 ……………………8分
当n≥2时,
[h (x)] n-h (x n)=(x+)n-(x n+)
=[(x n-2+)+(x n-4+)+…+(x n-2+) ]. ……………10分
由已知x>0,[h (x)] n-h (x n)≥++…+=2n-2,
∴[h (x)] n+2≥h (x n)+2 n ……………………12分