大余中学2006―2007学年高三(上)第四次月考数学(理科)试题
命题:黄小恩 卢岩松 梁模扬
一、选择题:本大题共12小题,每小题5分,共60分.
1、不等式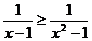 的解集为( )
的解集为( )
A.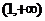 B.
B. C.
C.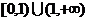 D.
D.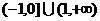
2、已知=(1,2), =(x,1),且+2与2-平行,则x等于( )
A.1
B.
3、已知命题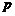 :x<-3是|x+1|>2的充分不必要条件;
:x<-3是|x+1|>2的充分不必要条件;
命题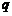 :在
:在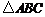 中,如果
中,如果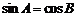 ,那么
,那么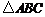 为直角三角形.则( )
为直角三角形.则( )
A.“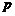 或
或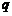 ”为假 B.“
”为假 B.“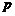 且
且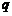 ”为真 C.
”为真 C.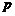 假
假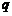 真 D.
真 D.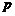 真
真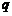 假
假
4、已知等差数列 的公差
的公差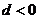 ,若
,若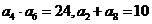 ,则该数列的前
,则该数列的前 项和
项和 的最大值是( )
的最大值是( )
A.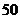 B.
B.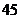 C.
C.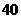 D.
D.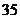
5、复数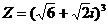 等于( )
等于( )
A.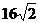 B.
B.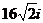 C.
C.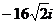 D.
D.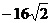
6、函数y = (0<a<1)的图象的大致形状是( )
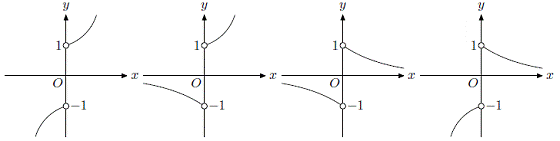 A
B
C
D
A
B
C
D
7、设集合M={平面内的点(a,b)},N={f(x)|f(x)=acos2x+bsin2x,x∈R},给出从M到N的映射f:(a,b)→f(x)=acos2x+bsin2x,则点(1,) 的象f(x)的最小正周期为( )
A.p B.
8、已知两点A(3,2)和B(-1,4)到直线mx + y + 3 = 0距离相等,则m值为( )
A.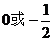 B.
B.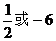 C.
C.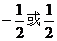 D.
D.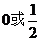
9、已知f(x)=sin(x+),g(x)=cos(x-),则下列结论中正确的是( )
A.函数y=f(x)?g(x)的周期为2π B.函数y=f(x)?g(x)的最大值为1
C.将f(x)的图象向右平移单位后得g(x)的图象
D.将f(x)的图象向左平移单位后得g(x)的图象
10、设向量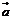 、
、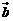 的模分别等于4、1,
的模分别等于4、1, 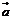 与
与 的夹角为,则
的夹角为,则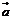 在
在 方向上的投影为( )
方向上的投影为( )
A.-2
B.
11、如果函数y = f(x-1)的反函数是y = f -1(x-1),则下列等式中正确的是( )
A.f(x)=f(x-1) B. f(x) - f(x-1) = 1
C.f(x) - f(x-1) = -1 D.f(x)=- f(x-1)
12、已知定义在R上的函数y=f(x)满足以下三个条件:
①对于任意的x∈R,都有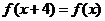 ;
;
②对于任意的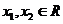 ,且
,且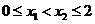 ,都有f (x1)<f
(x2);
,都有f (x1)<f
(x2);
③函数y=f (x+2)的图象关于y轴对称. 则下列结论中正确的是( )
A.f (4.5)<f (7)<f (6.5) B.f (7)<f (4.5)<f (6.5)
C.f (7)<f (6.5)<f (4.5) D.f (4.5)<f (6.5)<f (7)
二、填空题:本大题共4小题,每小题4分,共16分.将正确答案填在题中横线上.
13、设3sin2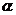 +2sin2
+2sin2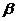 = 2sin
= 2sin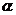 ,则函数y=sin2
,则函数y=sin2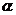 + sin 2
+ sin 2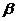 的值域为__________.
的值域为__________.
14、设x、y满足约束条件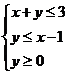 ,则z=x2+y2的最小值是___________.
,则z=x2+y2的最小值是___________.
15、有一排标号为A、B、C、D、E、F的6个座位,请2个家庭共6人入座,要求每个家庭的任何两个人不坐在一起,则不同的入座方法的总数为______.(用数字做答)
16、下列四个命题:①分别和两条异面直线均相交的两条直线一定是异面直线;
②一个平面内任意一点到另一个平面之距离均相等,那么这两个平面平行;
③一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角的平面角相等或互补;
④过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交.
其中正确命题的编号是 .
三、解答题(共6小题74分)
17、(满分12分)A、B、C为△ABC的三内角,且其对边分别为a、b、c.若=(-cos,sin),
=(cos,sin),且?=.
(1)求角A的大小;
(2)若a=2,△ABC面积S=,求b+c的值.
18、(满分12分)甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92.
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数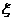 的数学期望.
的数学期望.
19、(满分12分)圆经过点A(2,-3)和B(-2,-5).
(1)若圆的面积最小,求圆的方程;
(2)若圆心在直线x-2y-3=0上,求圆的方程.
20、(满分12分)如图,在棱长为1的正方体ABCD―A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.
 (1)试确定点F的位置,使得D1E⊥平面AB1F;
(1)试确定点F的位置,使得D1E⊥平面AB1F;
(2)当D1E⊥平面AB1F时,求二面角C1―EF―A的大小.
21、(满分12分)已知函数f(x)=2x - .
(1)将y=f(x)的图象向右平移两个单位,得到函数y=g(x),求y=g(x)的解析式;
(2)函数y=h(x)与函数y=g(x)的图象关于直线y=1对称,求y=h(x)的解析式;
(3)设F(x) = f(x)+ h(x),F(x)的最小值是m,且m>2+,求实数a的取值范围.
22、(满分14分)某公司现有资金 万元,计划正式运营后的第一年资金将增长已有资金的25%,以后每年的资金增长量都将为上一年底剩余资金的25%,八年内公司每年均要支出各类资金固定为
万元,计划正式运营后的第一年资金将增长已有资金的25%,以后每年的资金增长量都将为上一年底剩余资金的25%,八年内公司每年均要支出各类资金固定为 万元,设
万元,设 为正式运营后第
为正式运营后第 年底的剩余资金.
年底的剩余资金.
(1)求 的表达式并加以证明;
的表达式并加以证明;
(2)只要八年内该公司每年的剩余资金都不少于 万元,八年后公司将形成规模并会长期运营,问如果
万元,八年后公司将形成规模并会长期运营,问如果 该公司能否长期运营,如果可以请加以证明,如果不行请说明理由.
该公司能否长期运营,如果可以请加以证明,如果不行请说明理由.
(取 )
)