高考数学第一轮复习--归纳―猜想―证明
(一)知识归纳:
由事物的部分特殊事例猜想出事物的一般结论,这种方法人们称为“不完全归纳法”,用不完全归纳法得出的结论需要经过证明,因此全部过程可以小结为下面程序:
①计算命题取特殊值时的结论;②对这些结果进行分析,探索数据的变化规律,并猜想命题的一般结论;③证明所猜想的结论.
(二)学习要点:
在中学数学内,“归纳―猜想―证明”的推理方法一般只局限于数列的内容,而且与正整数n有关,其它内容中很少有要求,解决问题时要注意以下几点,①计算特例时,不仅仅是简单的算数过程,有时要通过计算过程发现数据的变化规律;②猜想必须准确,绝对不能猜错,否则将徒劳无功;③如果猜想出来的结论与正整数n有关,一般用数学归纳法证明.
【例1】已知数列 满足关系式
满足关系式 N+),
N+),
(Ⅰ)用a表法a2,a3,a4;
(Ⅱ)猜想an的表达式(用a和n表示),并证明你的结论.
[解析](Ⅰ)
(Ⅱ)( ) 猜想
) 猜想 下面用数学归纳法证明:
下面用数学归纳法证明:
1°.当n=1时, 当n=1结论正确;
当n=1结论正确;
2°.假设当n=k时结论正确,即 ,
,
∴当n=k+1时 
= 当n=k+1时结论也正确;
当n=k+1时结论也正确;
根据1°与2°命题对一切n∈N*都正确.
[评析]“归纳―猜想―证明”是解决数列的某些问题的一种重要方法,对于一些变换技巧比较高的问题,如果能通过这种方法解答成功,则解答过程比较其它方法更容易.
【例2】已知数列 满足:
满足: 计算a2,a3,a4的值,由此归纳出an的公式,并证明你的结论.
计算a2,a3,a4的值,由此归纳出an的公式,并证明你的结论.
[解析]很容易算出a2=5,a3=16,a4=44,但由此猜想出结论显然是非常困难的,下面作一些探索.
∵a2=2 a1+3×2°=2×1+3×2°,
a3=2(2×1+3×2°)+3×21=22×1+2×3×21,
a4=2(22×1+2×3×21)+3×22=23×1+3×3×22;
猜想an=2n-1+(n-1)×3×2n-2=2n-2(3n-1);
用数学归纳法证明:
1°.当n=1时,a1=2-1×=1,结论正确;
2°.假设n=k时,ak=2k-2(3k-1)正确,
∴当n=k+1时, =
=
 结论正确;
结论正确;
由1°、2°知对n∈N*有
[评析]如果计算出来的数据很难猜出结论时,应考虑整理计算过程,探索数据的变化规律,看看能否猜想成功.
【例3】已知等差数列 中,a2=8,前10项的和S10=185,
中,a2=8,前10项的和S10=185,
(Ⅰ)求数列 的通项公式an;
的通项公式an;
(Ⅱ)若从数列 中依次取出第2,4,8,…,2n,…项,按原来的顺序排成一个新数列,试求新数列的前n项和An;
中依次取出第2,4,8,…,2n,…项,按原来的顺序排成一个新数列,试求新数列的前n项和An;
(Ⅲ)设 Bn=n(5+3 an),试比较An和Bn的大小,并说明理由.
[解析](Ⅰ)设公差为d,∴
(Ⅱ)设新数列为 ,∴
,∴
∴An=3×(2+22+23+…+2n)+2n=3×2n+1+2n-6;
(Ⅲ)∵
A4=3×32+2=98,A5=3×64+4=196,A6=3×128+6=390,A7=3×256+8=776,……
而B1=20,B2=58,B3=114,B4=188,B5=280,B6=390,B7=518,……
①当n=1,2,3,4,5时,Bn>An;
②当n=6时,B6=A6;
③当n≥7,且n∈N*时,猜想An>Bn,用数学归纳法证明:
1°.当n=7时,A7=766>518=B7,结论正确;
2°.假设当n=k(k≥7)时,Ak>Bk,即3×2k+1+2k-6>9k2+11k 2k+1>3k2+3k+2,
2k+1>3k2+3k+2,
∴n=k+1时,
=6×2 k+2-9k2-27k-24
=6×[2 k+1-(3k2+3k+2)]+6×(3k2+3k+2)-9k2-27k-24
=6×[2 k+1-(3k2+3k+2)]+9k2-9k-12
>9k2-9k-12=9k(k-1)-12≥9×7×(7-1)-12>0
∴Ak+1>Bk+1,即n=k+1时,结论也正确;
根据1°、2°知当n≥7且n∈N*时,有An>Bn.
[评析]从上面例子可以看出,归纳猜想不仅仅是要有对数据的观察能力,还需要有一定的经验,否则很难作出上述准确的猜想.
【例4】已知数列 满足:
满足: 问是否存在常数p、q,使得对一切n∈N*都有
问是否存在常数p、q,使得对一切n∈N*都有 并说明理由.
并说明理由.
[解析] ∵ 设存在这样的常数p、q,
设存在这样的常数p、q,
∴ 由此猜想,对n∈N*,有
由此猜想,对n∈N*,有
下面用数学归纳法证明这个结论:
1°.当n=1时, ,结论正确;
,结论正确;
2°.假设当n=k时结论正确,即 ∴当n=k+1时,
∴当n=k+1时,

∴当n=k+1时结论正确,故当n∈N*时, 成立.
成立.
[评析]例4是一类探索题型,由条件直接推出结论是非常困难的,通过归纳―猜想―证明的方法,难度不大.
《训练题》
一、选择题
1. 已知数列 的前n项和
的前n项和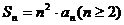 ,而
,而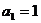 ,通过计算
,通过计算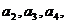 猜想
猜想
( )
A.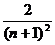 B.
B.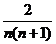 C.
C.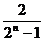 D.
D.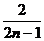
2.已知数列 的通项公式
的通项公式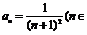 N*),记
N*),记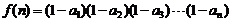 ,
,
通过计算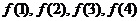 的值,由此猜想
的值,由此猜想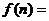 ( )
( )
A.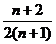 B.
B.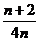 C.
C.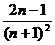 D.
D.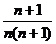
3.数列 中,a1=1,Sn表示前n项和,且Sn,Sn+1,2S1成等差数列,通过计算S1,S2,
中,a1=1,Sn表示前n项和,且Sn,Sn+1,2S1成等差数列,通过计算S1,S2,
S3,猜想Sn= ( )
A.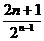 B.
B.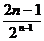 C.
C.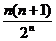 D.1-
D.1-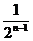
4.已知a1=1,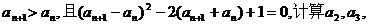 然后猜想
然后猜想
( )
A.n B.n2 C.n3 D.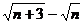
5.设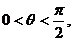 已知
已知 则猜想
则猜想 ( )
( )
A.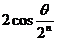 B.
B.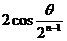 C.
C.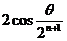 D.
D.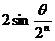
6.从一楼到二楼的楼梯共有n级台阶,每步只能跨上1级或2级,走完这n级台阶共有
种走法,则下面的猜想正确的是 ( )
A.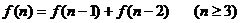 B.
B.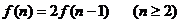
C.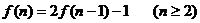 D.
D.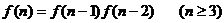
二、填空题:
7.已知数列 中,
中, 通过计算
通过计算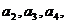 然后猜想
然后猜想
8.在数列 中,
中,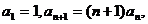 通过计算
通过计算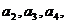 然后猜想
然后猜想
9.设数列 的前n项和为Sn,已知Sn=2n-an(n∈N+),通过计算数列的前四项,猜想
的前n项和为Sn,已知Sn=2n-an(n∈N+),通过计算数列的前四项,猜想

10.已知函数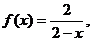 记数列
记数列 的前n项和为Sn,且
的前n项和为Sn,且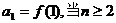 时,
时,
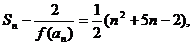 则通过计算
则通过计算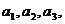 的值,猜想
的值,猜想 的通项公式
的通项公式
三、解答题
11.是否存在常数a,b,c,使等式
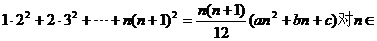 N+都成立,并证明你的结论.
N+都成立,并证明你的结论.
12.已知数列 的各项为正数,其前n项和为Sn,又
的各项为正数,其前n项和为Sn,又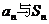 满足关系式:
满足关系式:
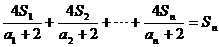 ,试求
,试求 的通项公式.
的通项公式.
13.已知数列 的各项为正数,Sn为前n项和,且
的各项为正数,Sn为前n项和,且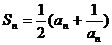 ,归纳出an的公式,并证明你的结论.
,归纳出an的公式,并证明你的结论.
14.已知数列 是等差数列,
是等差数列,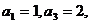 设
设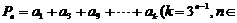 N+),
N+),
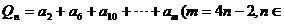 N+),问Pn与Qn哪一个大?证明你的结论.
N+),问Pn与Qn哪一个大?证明你的结论.
15.已知数列 :
: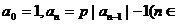 N*
N* 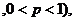
(Ⅰ)归纳出an的公式,并证明你的结论;
(Ⅱ)求证:
答案与解析
一、1.B 2.A 3.D 4.B 5.B 6.A
二、7.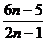 8.n! 9.
8.n! 9.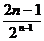 10.n+1
10.n+1
11.令n=1得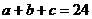 ①, 令n=2得
①, 令n=2得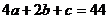 ②,
②,
令n=3得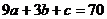 ③, 解①、②、③得a=3,b=11,c=10,记原式的左边为Sn,用数学归纳法证明猜想
③, 解①、②、③得a=3,b=11,c=10,记原式的左边为Sn,用数学归纳法证明猜想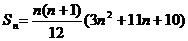 (证明略)
(证明略)
12.计算得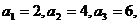 猜测
猜测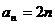 ,用数学归纳法证明(证明略).
,用数学归纳法证明(证明略).
13.∵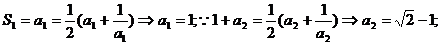
∵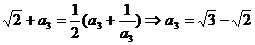 ,…,猜想
,…,猜想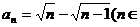 N*).用数学归纳法证明(略).
N*).用数学归纳法证明(略).
14.∵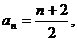 ∴
∴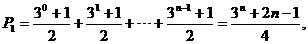
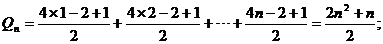 计算得①
计算得①
当1≤n≤3时,Pn<Qn;②猜想n≥4时Pn>Qn,用数学归纳法证明,即证:当n≥4时
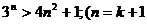 时用比较法证)
时用比较法证)
15.(Ⅰ)∵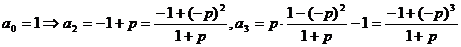 ,…,猜测
,…,猜测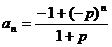 ,数学归纳法证明(略).
,数学归纳法证明(略).
(Ⅱ)∵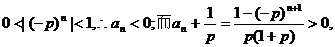
∴