网址:http://m.1010jiajiao.com/timu_id_24028[举报]
已知函数 =
= .
.
(Ⅰ)当 时,求不等式
时,求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
【命题意图】本题主要考查含绝对值不等式的解法,是简单题.
【解析】(Ⅰ)当 时,
时, =
= ,
,
当 ≤2时,由
≤2时,由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
当2< <3时,
<3时, ≥3,无解;
≥3,无解;
当 ≥3时,由
≥3时,由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集为{
≥3的解集为{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
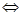
 ,
,
当 ∈[1,2]时,
∈[1,2]时, =
= =2,
=2,
∴ ,有条件得
,有条件得 且
且 ,即
,即 ,
,
故满足条件的 的取值范围为[-3,0]
的取值范围为[-3,0]
查看习题详情和答案>>
已知数列 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d, 为其前n项和,且满足
为其前n项和,且满足 ,
, .数列
.数列 满足
满足 ,
, ,
, 为数列
为数列 的前n项和.
的前n项和.
(1)求数列 的通项公式
的通项公式 和数列
和数列 的前n项和
的前n项和 ;
;
(2)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在正整数
 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问利用在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 时,
时, 满足
满足 ,
,
 ,
,

第二问,①当n为偶数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等号在n=2时取得.
,等号在n=2时取得.
 此时
此时 需满足
需满足 .
.
②当n为奇数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是随n的增大而增大, n=1时
是随n的增大而增大, n=1时 取得最小值-6.
取得最小值-6.
 此时
此时 需满足
需满足 .
.
第三问 ,
,
若 成等比数列,则
成等比数列,则 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
(1)(法一)在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 时,
时, 满足
满足 ,
,
 ,
,
 .
.
(2)①当n为偶数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等号在n=2时取得.
,等号在n=2时取得.
 此时
此时 需满足
需满足 .
.
②当n为奇数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是随n的增大而增大, n=1时
是随n的增大而增大, n=1时 取得最小值-6.
取得最小值-6.
 此时
此时 需满足
需满足 .
.
综合①、②可得 的取值范围是
的取值范围是 .
.
(3) ,
,
若 成等比数列,则
成等比数列,则 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
又 ,且m>1,所以m=2,此时n=12.
,且m>1,所以m=2,此时n=12.
因此,当且仅当m=2,
n=12时,数列 中的
中的 成等比数列
成等比数列
查看习题详情和答案>>
4. m>2或m<-2 解析:因为f(x)=![]() 在(-1,1)内有零点,所以f(-1)f(1)<0,即(2+m)(2-m)<0,则m>2或m<-2
在(-1,1)内有零点,所以f(-1)f(1)<0,即(2+m)(2-m)<0,则m>2或m<-2
随机变量![]() 的所有等可能取值为1,2…,n,若
的所有等可能取值为1,2…,n,若![]() ,则( )
,则( )
A. n=3 B.n=4 C. n=5 D.不能确定
5.m=-3,n=2 解析:因为![]() 的两零点分别是1与2,所以
的两零点分别是1与2,所以![]() ,即
,即![]() ,解得
,解得![]()
6.![]() 解析:因为
解析:因为![]() 只有一个零点,所以方程
只有一个零点,所以方程![]() 只有一个根,因此
只有一个根,因此![]() ,所以
,所以![]()
袋子中装有大小形状完全相同的m个红球和n个白球,其中m,n满足m>n≥2且m+n≤l0(m,n∈N+),若从中取出2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m,n的值;
(Ⅱ) 从袋子中任取3个球,设取到红球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
【解析】第一问中利用 ,解得m=6,n=3.
,解得m=6,n=3.
第二问中, 的取值为0,1,2,3. P(
的取值为0,1,2,3. P( =0)=
=0)= 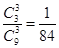 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
得到分布列和期望值
解:(I)据题意得到 解得m=6,n=3.
解得m=6,n=3.
(II) 的取值为0,1,2,3.
的取值为0,1,2,3.
P( =0)=
=0)= 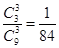 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
 的分布列为
的分布列为

所以E =2
=2
查看习题详情和答案>>
已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1, )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数 的取值范围。
的取值范围。
【解析】本试题中导数在研究函数中的运用。(1)中 ,那么当
,那么当 时,
时, 又
又  所以函数
所以函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 ;(2)中令
;(2)中令 有
有 

对a分类讨论 ,和
,和 得到极值。(3)中,设
得到极值。(3)中,设 ,
, ,依题意,只需
,依题意,只需 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 
∴ 当 时,
时, 又
又 
∴ 函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 --------4分
--------4分
(Ⅱ)令 有
有 

①
当 即
即 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是 ,极小值是
,极小值是
②
当 即
即 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为 ,无极小值。
,无极小值。
综上所述  时,极大值为
时,极大值为 ,无极小值
,无极小值
 时 极大值是
时 极大值是 ,极小值是
,极小值是 ----------8分
----------8分
(Ⅲ)设 ,
,
对 求导,得
求导,得
∵ ,
,

∴  在区间
在区间 上为增函数,则
上为增函数,则
依题意,只需 ,即
,即
解得  或
或 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(
 ,
, )
)
查看习题详情和答案>>

 )
)

