摘要:(Ⅱ)求证: 答案与解析
网址:http://m.1010jiajiao.com/timu_id_24024[举报]
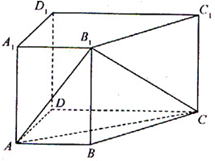
如图,在四棱柱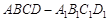 中,侧棱
中,侧棱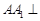 底面
底面 ,
,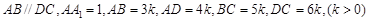
(Ⅰ)求证: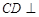 平面
平面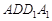
(Ⅱ)若直线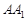 与平面
与平面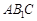 所成角的正弦值为
所成角的正弦值为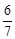 ,求
,求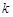 的值
的值
(Ⅲ)现将与四棱柱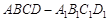 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为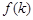 ,写出
,写出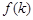 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)
查看习题详情和答案>>
如图,在四棱柱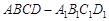 中,侧棱
中,侧棱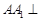 底面
底面 ,
,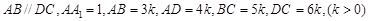
(Ⅰ)求证: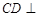 平面
平面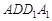
(Ⅱ)若直线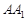 与平面
与平面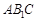 所成角的正弦值为
所成角的正弦值为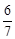 ,求
,求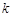 的值
的值
(Ⅲ)现将与四棱柱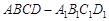 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为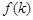 ,写出
,写出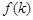 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)
如图,在四棱柱 中,侧棱
中,侧棱 底面
底面 ,
,

(Ⅰ)求证: 平面
平面
(Ⅱ)若直线 与平面
与平面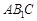 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值
(Ⅲ)现将与四棱柱 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出
,写出 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)
 中,侧棱
中,侧棱 底面
底面 ,
,

(Ⅰ)求证:
 平面
平面
(Ⅱ)若直线
 与平面
与平面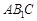 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值(Ⅲ)现将与四棱柱
 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出
,写出 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由) ,求k的值
,求k的值
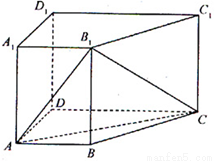
 (2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)