题目内容
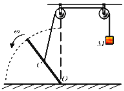
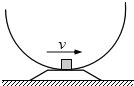
【题目】如图所示,半径为R的半球形碗固定于水平地面上,一个质量为m的物块,从碗口沿内壁由静止滑下,滑到最低点时速度大小为v,物块与碗之间的动摩擦因数恒为ì,则下列说法正确的是( )
A.在最低点时物块所受支持力大小为mg
B.整个下滑过程物块所受重力的功率先增大后减小
C.物块在下滑至最低点过程中动能先增大后减小
D.整个下滑过程滑块克服摩擦力做功为![]()
【答案】BCD
【解析】
A.在最低点时,根据牛顿第二定律得,
N﹣mg=m![]()
解得支持力
N=mg+m![]()
故A错误。
B.初始位置物体的速度为零,重力的瞬时功率为零。到达最低点时,重力与速度的方向夹角为![]() ,重力的瞬时功率也为零,可知整个过程中功率的功率先增大后减小。故B正确。
,重力的瞬时功率也为零,可知整个过程中功率的功率先增大后减小。故B正确。
C.在下滑的过程中,重力沿曲面切线方向的分力逐渐减小,滑动摩擦力逐渐增大,开始阶段,重力的切向分力大于摩擦力,物体做加速运动,动能增大,之后,重力的切向分力小于摩擦力,做减速运动,动能减小,则动能先增大后减小。故C正确。
D.对整个过程运用动能定理得
mgR﹣Wf=![]() mv2﹣0
mv2﹣0
则滑块克服摩擦力做功为
Wf=mgR﹣![]() mv2
mv2
故D正确。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目