题目内容
质量为m的登月器与航天飞机连接在一起 ,随航天飞机绕月球做半径为3R( R为月球半径)的圆周运动。当它们运行到轨道的A点时,登月器被弹离, 航天飞机速度变大,登月器速度变小且仍沿原方向运动,随后登月器沿椭圆登上月球表面的B点,在月球表面逗留一段时间后,经快速起动仍沿原椭圆轨道回到分离点A与航天飞机实现对接。已知月球表面
,随航天飞机绕月球做半径为3R( R为月球半径)的圆周运动。当它们运行到轨道的A点时,登月器被弹离, 航天飞机速度变大,登月器速度变小且仍沿原方向运动,随后登月器沿椭圆登上月球表面的B点,在月球表面逗留一段时间后,经快速起动仍沿原椭圆轨道回到分离点A与航天飞机实现对接。已知月球表面 的重力加速度为g月。科学研究表明,天体在椭圆轨道
的重力加速度为g月。科学研究表明,天体在椭圆轨道
上运行的周期的平方与轨道半长轴的立方成正比。试求:
(1)登月器与航天飞机一起在圆周轨道上绕月球运行的周期是多少?
(2)若登月器被弹射后,航天飞机的椭圆轨道长轴为8R,则为保证登月器能顺利返回A点,登月器可以在月球表面逗留的时间是多少?
 ,随航天飞机绕月球做半径为3R( R为月球半径)的圆周运动。当它们运行到轨道的A点时,登月器被弹离, 航天飞机速度变大,登月器速度变小且仍沿原方向运动,随后登月器沿椭圆登上月球表面的B点,在月球表面逗留一段时间后,经快速起动仍沿原椭圆轨道回到分离点A与航天飞机实现对接。已知月球表面
,随航天飞机绕月球做半径为3R( R为月球半径)的圆周运动。当它们运行到轨道的A点时,登月器被弹离, 航天飞机速度变大,登月器速度变小且仍沿原方向运动,随后登月器沿椭圆登上月球表面的B点,在月球表面逗留一段时间后,经快速起动仍沿原椭圆轨道回到分离点A与航天飞机实现对接。已知月球表面 的重力加速度为g月。科学研究表明,天体在椭圆轨道
的重力加速度为g月。科学研究表明,天体在椭圆轨道上运行的周期的平方与轨道半长轴的立方成正比。试求:
(1)登月器与航天飞机一起在圆周轨道上绕月球运行的周期是多少?
(2)若登月器被弹射后,航天飞机的椭圆轨道长轴为8R,则为保证登月器能顺利返回A点,登月器可以在月球表面逗留的时间是多少?

(1)设登月器和航天飞机在半径3R的轨道上运行时的周期为T,因其绕月球作圆周运动,所以应满足 -------------①
-------------①
同时月球表面的物体所受重力和引力的关系满足 --------------②
--------------②
联立①②得 --------------③ (4分)
--------------③ (4分)
(2)设登月器在小椭圆轨道运行的周期是T1,航天飞机在大椭圆轨道运行的周期是T2。对登月器依题意有: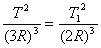 ------④
------④
解得 -----⑤(2分)
-----⑤(2分)
对航天飞机依题意有: -----------⑥
-----------⑥
解得 ------⑦(2分)
------⑦(2分)
为使经登月器仍沿原椭圆轨道回到分离点与航天飞机实现对接,登月器可以在月球表面逗留的时间t应满足:t="nT2-T1" (其中,n=1、2、3、)-----⑧
联立③⑤⑦⑧得


 (其中,n=1、2、3、) (4分)
(其中,n=1、2、3、) (4分)
 -------------①
-------------①同时月球表面的物体所受重力和引力的关系满足
 --------------②
--------------②联立①②得
 --------------③ (4分)
--------------③ (4分)(2)设登月器在小椭圆轨道运行的周期是T1,航天飞机在大椭圆轨道运行的周期是T2。对登月器依题意有:
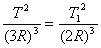 ------④
------④解得
 -----⑤(2分)
-----⑤(2分)对航天飞机依题意有:
 -----------⑥
-----------⑥解得
 ------⑦(2分)
------⑦(2分)为使经登月器仍沿原椭圆轨道回到分离点与航天飞机实现对接,登月器可以在月球表面逗留的时间t应满足:t="nT2-T1" (其中,n=1、2、3、)-----⑧
联立③⑤⑦⑧得



 (其中,n=1、2、3、) (4分)
(其中,n=1、2、3、) (4分)略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






