题目内容
3. 如图,一束电子(电量为e)以速度v从A点垂直射入磁感强度为B,宽度为d的匀强磁场中,在B点穿出磁场,速度方向与电子原来入射方向的夹角是30°,求:
如图,一束电子(电量为e)以速度v从A点垂直射入磁感强度为B,宽度为d的匀强磁场中,在B点穿出磁场,速度方向与电子原来入射方向的夹角是30°,求:①轨迹的半径r
②电子的质量m
③电子在磁场中的时间t.
分析 ①作出电子的运动轨迹,由几何知识可以求出电子的轨道半径;
②电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出电子质量;
③求出电子在磁场中转过的圆心角,然后求出其运动时间.
解答 解:①电子在磁场中做匀速圆周运动,其运动轨迹如图所示: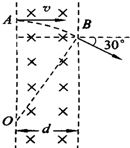
由几何知识可得,电子轨道半径:
r=$\frac{d}{sin30°}$=2d;
②电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:evB=m$\frac{{v}^{2}}{r}$,
解得电子质量:m=$\frac{2eBd}{v}$;
③电子在磁场中故可求得m=2eBd/v.
电子在磁场中转过的圆心角:θ=30°,
电子在磁场中的运动时间:t=$\frac{θ}{360°}$T=$\frac{30°}{360°}$×$\frac{2πm}{eB}$=$\frac{πd}{3v}$;
答:①轨迹的半径r为2d;
②电子的质量m为$\frac{2eBd}{v}$;
③电子在磁场中的时间t为$\frac{πd}{3v}$.
点评 本题考查了电子在磁场中的运动,分析清楚电子运动过程、作出电子的运动轨迹是正确解题的关键,应用几何知识、牛顿第二定律与电子做圆周运动的周期公式可以解题.

练习册系列答案
相关题目
13.欲划船渡过一宽100m的河,船相对静水速度v1=5m/s,水流速度v2=8m/s,则( )
| A. | 过河最短时间为20s | B. | 过河位移最短所用的时间是25s | ||
| C. | 过河最短时间为25s | D. | 过河位移最短所用的时间是20s |
11. 2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
 2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )| A. | 卫星“G1”和“G3”的加速度大小相等均为 $\frac{{R}^{2}}{r}$g | |
| B. | 卫星“G1”由位置A运动到位置B所需的时间为$\frac{2πr}{3R}$$\sqrt{\frac{r}{g}}$ | |
| C. | 如果调动“高分一号”卫星到达卫星“G3”所在的轨道,必须对其减速 | |
| D. | “高分一号”是低轨道卫星,其所在高度有稀薄气体,运行一段时间后,高度会降低,速度增大,机械能会减小 |
8.2001年10月21日零时起,我国铁路进行第四次提速.通常提速要解决许多技术问题.已知列车所受阻力与速度成正比,及f=kv.当机车以40km/h匀速行驶时功率为P,当机车以速度120km/h匀速行驶时功率为( )
| A. | 9P | B. | 27P | C. | 4P | D. | 不变 |
12.电磁感应对社会贡献巨大,第一个发现电磁感应的科学家是( )
| A. | 奥斯特 | B. | 安培 | C. | 法拉第 | D. | 欧姆 |
 辩析题:在如图所示电路中,电源电动势E=6V,内阻不计,小灯L上标有“6V,0.3A”字样,滑动变阻器R1的阻值范围是0-20Ω,电阻R2上标有“15Ω,4A”,电流表的量程为0-0.6A.甲、乙两同学在讨论滑动变阻器功率的取值范围时,甲同学认为:由于电流表允许通过的最大电流为0.6A,所以通过R1的最大电流为0.3A,这时滑动变阻器R1两端的电压为U1m=E-I1mR2=1.5V,因此滑动变阻器的最大功率为P1m=I1mU1m=0.45W.乙同学不同意甲同学的看法,他认为滑动变阻器的功率决定于通过它的电流和它两端的电压的乘积,即P1=I1U1,电流最大时功率未必最大,只有电流、电压的乘积最大时,功率才最大.
辩析题:在如图所示电路中,电源电动势E=6V,内阻不计,小灯L上标有“6V,0.3A”字样,滑动变阻器R1的阻值范围是0-20Ω,电阻R2上标有“15Ω,4A”,电流表的量程为0-0.6A.甲、乙两同学在讨论滑动变阻器功率的取值范围时,甲同学认为:由于电流表允许通过的最大电流为0.6A,所以通过R1的最大电流为0.3A,这时滑动变阻器R1两端的电压为U1m=E-I1mR2=1.5V,因此滑动变阻器的最大功率为P1m=I1mU1m=0.45W.乙同学不同意甲同学的看法,他认为滑动变阻器的功率决定于通过它的电流和它两端的电压的乘积,即P1=I1U1,电流最大时功率未必最大,只有电流、电压的乘积最大时,功率才最大. 如图所示,ef、gh为两水平放置的相互平行的金属导轨,ab、cd为搁在导轨上的两金属棒,与导轨接触良好且无摩擦.当一个N极朝下的条形磁铁从某一高度自由下落向下靠近导轨时,则四根导体棒形成的闭合回路的磁通量增加(填“增加”、“减小”或“不变”),此时产生的感应磁场与原磁场反向(填“同向”或“反向”),由安培定则可以得出感应电流的方向是acdb(填“abdc”或“acdb”)
如图所示,ef、gh为两水平放置的相互平行的金属导轨,ab、cd为搁在导轨上的两金属棒,与导轨接触良好且无摩擦.当一个N极朝下的条形磁铁从某一高度自由下落向下靠近导轨时,则四根导体棒形成的闭合回路的磁通量增加(填“增加”、“减小”或“不变”),此时产生的感应磁场与原磁场反向(填“同向”或“反向”),由安培定则可以得出感应电流的方向是acdb(填“abdc”或“acdb”)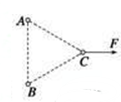 光滑绝缘的水平面上固定着三个带电小球A、B、C,它们的质量均为m,间距均为r,A、B带等量正电荷q,现对C球施一水平力F的同时,将三个小球都放开,如图所示,欲使得三个小球在运动过程中保持间距r不变,求:
光滑绝缘的水平面上固定着三个带电小球A、B、C,它们的质量均为m,间距均为r,A、B带等量正电荷q,现对C球施一水平力F的同时,将三个小球都放开,如图所示,欲使得三个小球在运动过程中保持间距r不变,求: