题目内容
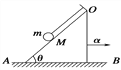
【题目】如图所示两个半径分别为RA=1m、RB=2m的金属圆环处在竖直向下、磁感应强度B1=1T的环形匀强磁场中，一根长L=2m、阻值为2Ω的均匀金属棒OB跨放在两金属圆环上，且O点位于两环的圆心处。另有两根间距l=1m、足够长的“L”形光滑金属导轨与水平面成θ=30°角倾斜放置，在导轨下端的挡板上，静放着一根长l=lm、质量m=0.1kg、阻值R=1Ω的金属棒CD，倾斜导轨的上端通过两根导线分别与A、B两环相连，两导轨处在与导轨平面垂直斜向上、B2=1T的匀强磁场中，除两根金属样的电阻外，其余电阻均不计。t=0时金属OB在外作用下以角速度ω=2rad/s绕O点逆时针匀速转动，t=2s时金属棒CD刚好达到最大速度，若取g=10m/s2。
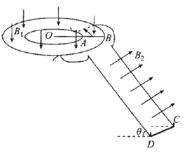
(1)求金属棒CD达到的最大速度；
(2)若t=2s时，因故障金属棒OB停止转动，金属棒CD继续上滑，现测得金属棒CD由t=0时刻至上滑到最高点的过程中通过的电量为1.3C，求故障后金属棒CD在上滑过程中产生的焦耳热。
【答案】(1) 
(2) 
【解析】
(1)金属棒OB匀速转动时切割磁感线产生感应电动势
又
，
，故E=3V且A环电势高，
金属棒OB切割磁感线对金属棒CD供电，金属棒CD向上做加速运动有
由于金属棒CD切割磁感线也产生电动势，回路中的有效电阻为2R=2
故
当金属棒CD的加速度减小到0时有最大速度
代入数据解得：
；
(2)金属棒CD加速上滑过程中由
解得：
金属棒CD减速上滑过程中通过的电量为
由
知金属棒CD沿导轨减速上滑的距离为
金属棒CD减速上滑过程中由能量守恒定律得：
代入数据解得：
.
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
