题目内容
6.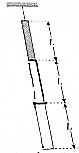 如图所示,一根长度为L的直轩用一细线悬挂于天花版上,在其正下方距直杆的下端L处有一长度也为L的空心直圆筒,圆筒内径略大于直杆的外径且距水平地面足够高,现将悬挂直杆的细线剪断,直杆自由落下,忽略空气阻力,重力加速度为g.
如图所示,一根长度为L的直轩用一细线悬挂于天花版上,在其正下方距直杆的下端L处有一长度也为L的空心直圆筒,圆筒内径略大于直杆的外径且距水平地面足够高,现将悬挂直杆的细线剪断,直杆自由落下,忽略空气阻力,重力加速度为g.(1)若圆筒固定,求直杆穿过圆筒所经历的时间t.
(2)若直杆刚进入圆筒时将圆筒也由静止释放,求直杆穿过圆筒的过程中,圆筒下落的高度h.
分析 (1)直杆从开始下落到其下端刚好进入圆筒,即下落位移为H,根据位移时间公式可求解,直杆从开始下落到其下端刚好穿出圆筒,根据位移时间公式可求解
(2)利用位移时间公式表示出两者通过的位移,即可求得位移
解答 解:(1)设直杆下端到达圆筒上方的时间为t1,L=12gt21L=12gt21
解得t1=√2Lg√2Lg
直杆上端离开圆筒下方时间为t,3L=12gt23L=12gt2
解得t=√6Lg√6Lg
直杆穿越圆筒所用的时间为
t2=t-t1=√6Lg−√2Lg√6Lg−√2Lg
(2)直杆刚进入圆筒时的速度为v,则v=gt1
根据位移时间公式可知杆下降的高度h1=v1t−12gt2h1=v1t−12gt2
筒下降的高度h2=12gt2h2=12gt2
h1-h2=2L
联立解得h2=L
答:(1)若圆筒固定,求直杆穿过圆筒所经历的时间t为√6Lg−√2Lg√6Lg−√2Lg.
(2)若直杆刚进入圆筒时将圆筒也由静止释放,直杆穿过圆筒的过程中,圆筒下落的高度h为L
点评 本题主要考查了自由落体运动的基本公式的直接应用,难度不大.

练习册系列答案
相关题目
16.一质点沿x轴运动,其位置x随时间t变化的规律为x=15+10t-5t2.下列关于该质点运动的说法正确的是( )
| A. | 该质点的加速度大小为5 m/s2 | |
| B. | t=3 s时刻该质点速度为零 | |
| C. | 0--3 s内该质点的平均速度大小为5 m/s | |
| D. | 物体处于x=0处时其速度大小为20 m/s |
7.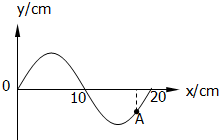 如图,为一列沿x轴正方向传播的简谐波在某时刻的波形图,A是参与波动的介质中的一个质点,若波源的振动周期为T=1s,则从该时刻起质点运动到平衡位置所需的时间可能为( )
如图,为一列沿x轴正方向传播的简谐波在某时刻的波形图,A是参与波动的介质中的一个质点,若波源的振动周期为T=1s,则从该时刻起质点运动到平衡位置所需的时间可能为( )
 如图,为一列沿x轴正方向传播的简谐波在某时刻的波形图,A是参与波动的介质中的一个质点,若波源的振动周期为T=1s,则从该时刻起质点运动到平衡位置所需的时间可能为( )
如图,为一列沿x轴正方向传播的简谐波在某时刻的波形图,A是参与波动的介质中的一个质点,若波源的振动周期为T=1s,则从该时刻起质点运动到平衡位置所需的时间可能为( )| A. | 0.1s | B. | 0.2s | C. | 0.3s | D. | 0.5s |
8.一个标明“1KΩ、40W”的电阻,表明( )
| A. | 额定电压是200V | B. | 允许长期通过它的电流是0.2A | ||
| C. | 在额定电压下的电功率是40W | D. | 加50V电压时实际电功率是10W |
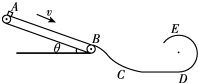 如图所示,传送带A、B之间的距离L=3.2m,与水平面夹角θ=37°,传送带沿顺时针方向转动,速度恒为v=2m/s,在上端A点无初速度放置一个质量为m=1kg、大小可视为质点的金属块,它与传送带的动摩擦因数为μ=0.5,金属块滑离传送带后经过弯道沿半径R=0.4m的光滑圆轨道做圆周运动,刚好能通过最高点E,已知B、D两点的竖直高度差为h=0.5m(g取10m/s2).求:
如图所示,传送带A、B之间的距离L=3.2m,与水平面夹角θ=37°,传送带沿顺时针方向转动,速度恒为v=2m/s,在上端A点无初速度放置一个质量为m=1kg、大小可视为质点的金属块,它与传送带的动摩擦因数为μ=0.5,金属块滑离传送带后经过弯道沿半径R=0.4m的光滑圆轨道做圆周运动,刚好能通过最高点E,已知B、D两点的竖直高度差为h=0.5m(g取10m/s2).求: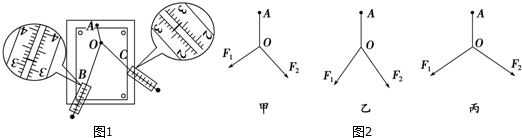
 电磁弹射器是航空母舰上的一种舰载机起飞装置,已由美国福特号航母首先装备,我国未来的航母将采用自行研制的电磁弹射器.电磁弹射系统包括电源、强迫储能装置、导轨和脉冲发生器等等.其工作原理可简化为如图所示;上下共4根导轨,飞机前轮下有一牵引杆,与飞机前轮连为一体,可收缩并放置在飞机的腹腔内.起飞前牵引杆伸出至上下导轨之间,强迫储能装置提供瞬发能量,强大的电流从导轨流经牵引杆,牵引杆在强大的安培力作用下推动飞机运行到高速.现有一弹射器弹射某飞机,设飞机质量m=2×104kg,起飞速度为v=60m/s,起飞过程所受到阻力恒为机重的0.2倍,在没有电磁弹射器的情况下,飞机从静止开始匀加速起飞,起飞距离为l=200m,在电磁弹射器与飞机的发动机(设飞机牵引力不变)同时工作的情况下,匀加速起飞距离减为50m,假设弹射过程强迫储能装置的能量全部转为飞机的动能.取g=10m/s2.求:
电磁弹射器是航空母舰上的一种舰载机起飞装置,已由美国福特号航母首先装备,我国未来的航母将采用自行研制的电磁弹射器.电磁弹射系统包括电源、强迫储能装置、导轨和脉冲发生器等等.其工作原理可简化为如图所示;上下共4根导轨,飞机前轮下有一牵引杆,与飞机前轮连为一体,可收缩并放置在飞机的腹腔内.起飞前牵引杆伸出至上下导轨之间,强迫储能装置提供瞬发能量,强大的电流从导轨流经牵引杆,牵引杆在强大的安培力作用下推动飞机运行到高速.现有一弹射器弹射某飞机,设飞机质量m=2×104kg,起飞速度为v=60m/s,起飞过程所受到阻力恒为机重的0.2倍,在没有电磁弹射器的情况下,飞机从静止开始匀加速起飞,起飞距离为l=200m,在电磁弹射器与飞机的发动机(设飞机牵引力不变)同时工作的情况下,匀加速起飞距离减为50m,假设弹射过程强迫储能装置的能量全部转为飞机的动能.取g=10m/s2.求: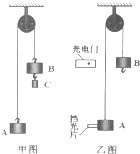 如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.