题目内容
3.同步卫星与地心的距离为r1,运行速率为v1,向心加速度为a1;近地卫星运行速率为v2,向心加速度为a2;地球赤道上的物体随地球自转的速率为v3,向心加速度为a3;地球半径为r,则下列比值正确的是( )①$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{r}{{r}_{1}}}$ ②$\frac{{v}_{1}}{{v}_{3}}$=$\frac{{r}_{1}}{r}$ ③$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}^{2}}{{{r}_{1}}^{2}}$ ④$\frac{{a}_{1}}{{a}_{3}}$=$\frac{{{r}_{1}}^{2}}{{r}^{2}}$.
| A. | ①③ | B. | ②④ | C. | ①③ | D. | ①② |
分析 同步卫星的角速度和地球自转的角速度相等,根据a=rω2得出物体随地球自转的向心加速度与同步卫星的加速度之比.根据万有引力提供向心力求出线速度与轨道半径的关系,从而求出近地卫星和同步卫星的线速度之比.
解答 解:①、根据万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$ 得:$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{r}{{r}_{1}}}$,故①正确,
②、同步卫星的角速度和地球自转的角速度相等,由v=ωr得:$\frac{{v}_{1}}{{v}_{3}}$=$\frac{{r}_{1}}{r}$.故②正确;
③、根据万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=ma,得:$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}^{2}}{{r}_{1}^{2}}$,故③错误;
④、同步卫星的角速度和地球自转的角速度相等,根据a=rω2得:$\frac{{a}_{1}}{{a}_{3}}$=$\frac{{r}_{1}}{r}$.故④错误;
故选:D.
点评 解决本题的关键知道同步卫星的特点,以及掌握万有引力提供向心力这一理论,并能灵活运用.

练习册系列答案
相关题目
13.一质点做简谐运动的图象如图所示,下列说法正确的是( )


| A. | 0~1s速度在增大 | B. | 0~1s位移在增大 | ||
| C. | 2~3s加速度在增大 | D. | 2~3s位移在增大 |
14.我国“玉兔号”月球车被顺利送抵月球表面,并发回大量图片和信息.若该月球车在地球表面的重力为G1,在月球表面的重力为G2.已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )
| A. | “玉兔号”月球车在地球表面与月球表面质量之比为1:1 | |
| B. | 地球的质量与月球的质量之比为$\frac{{G}_{1}{{R}_{2}}^{2}}{{G}_{2}{{R}_{1}}^{2}}$ | |
| C. | 地球表面处的重力加速度与月球表面处的重力加速度之比为$\frac{{G}_{2}}{{G}_{1}}$ | |
| D. | 地球的第一宇宙速度与月球的第一宇宙速度之比为$\sqrt{\frac{{G}_{1}{R}_{1}}{{G}_{2}{R}_{2}}}$ |
8.发射某探月卫星时,首先使其环绕地球表面做圆周运动,线速度为v1,环绕周期为T1,月球附近时,控制卫星使其绕月球表面做圆周运动,线速度为v2,环绕周期为T2,若两球的质量分别为M1,M2,则$\frac{{M}_{1}}{{M}_{2}}$( )
| A. | $\frac{{{T}_{1}v}_{2}}{{{T}_{2}v}_{1}}$ | B. | $\frac{{{T}_{1}v}_{2}^{3}}{{{T}_{2}v}_{1}^{3}}$ | ||
| C. | $\frac{{{T}_{1}v}_{1}}{{{T}_{2}v}_{2}}$ | D. | $\frac{{{T}_{1}v}_{1}^{3}}{{{T}_{2}v}_{2}^{3}}$ |
15. 如图,真空中有一个边长为L的正方体,正方体的两个顶点M、N处分别放置一对电荷量都为q的正、负点电荷.图中的a、b、c、d是其它的四个顶点,k为静电力常量,下列表述正确是( )
如图,真空中有一个边长为L的正方体,正方体的两个顶点M、N处分别放置一对电荷量都为q的正、负点电荷.图中的a、b、c、d是其它的四个顶点,k为静电力常量,下列表述正确是( )
 如图,真空中有一个边长为L的正方体,正方体的两个顶点M、N处分别放置一对电荷量都为q的正、负点电荷.图中的a、b、c、d是其它的四个顶点,k为静电力常量,下列表述正确是( )
如图,真空中有一个边长为L的正方体,正方体的两个顶点M、N处分别放置一对电荷量都为q的正、负点电荷.图中的a、b、c、d是其它的四个顶点,k为静电力常量,下列表述正确是( )| A. | a、b两点电场强度相同 | |
| B. | a点电势高于b点电势 | |
| C. | 把点电荷+Q从c移到d,电势能增加 | |
| D. | M点的电荷受到的库仑力大小为F=k$\frac{q^2}{{2{L^2}}}$ |
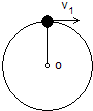 长度为L细绳,一端系有一质量为m的小球,小球以O点为圆心在竖直面内做圆周运动,求:
长度为L细绳,一端系有一质量为m的小球,小球以O点为圆心在竖直面内做圆周运动,求: 物体做圆周运动时所需的向心力F需由物体运动情况决定,合力提供的向心力F供由物体受力情况决定.若某时刻F需=F供,则物体能做圆周运动;若F需>F供,物体将做离心运动;若F需<F供,物体将做近心运动.现有一根长L=1m的刚性轻绳,其一端固定于O点,另一端系着质量m=0.5kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图所示.不计空气阻力,g取10m/s2,则:
物体做圆周运动时所需的向心力F需由物体运动情况决定,合力提供的向心力F供由物体受力情况决定.若某时刻F需=F供,则物体能做圆周运动;若F需>F供,物体将做离心运动;若F需<F供,物体将做近心运动.现有一根长L=1m的刚性轻绳,其一端固定于O点,另一端系着质量m=0.5kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图所示.不计空气阻力,g取10m/s2,则: 如图所示,在直角坐标系的第Ⅰ象限存在垂直纸面向里的匀强磁场,磁感应强度B=0.2T,第Ⅳ象限分布着竖直向上的匀强电场,场强E=4.0×103V/m.现从图中M(1.8,-1.0)点由静止释放一比荷$\frac{q}{m}$=2×105C/kg的带正电的粒子,该粒子经过电场加速后经x轴上的P点进入磁场,在磁场中运动一段时间后经y轴上的N点离开磁场.不计重力,求:
如图所示,在直角坐标系的第Ⅰ象限存在垂直纸面向里的匀强磁场,磁感应强度B=0.2T,第Ⅳ象限分布着竖直向上的匀强电场,场强E=4.0×103V/m.现从图中M(1.8,-1.0)点由静止释放一比荷$\frac{q}{m}$=2×105C/kg的带正电的粒子,该粒子经过电场加速后经x轴上的P点进入磁场,在磁场中运动一段时间后经y轴上的N点离开磁场.不计重力,求: