题目内容
5.有两个大小相同、同种材料组成的均匀球体紧靠在一起,它们之间的万有引力为F,若用上述材料制成两个半径更小的靠在一起的均匀球体,它们间的万有引力将( )| A. | 等于F | B. | 小于F | C. | 大于F | D. | 无法比较 |
分析 质量分布均匀的球体,可以用万有引力定律求球体间的万有引力,此时距离为两球球心间的距离,根据质量与半径的关系根据万有引力表达式求解.
解答 解:根据题意令材料的密度为ρ,则两球的质量分别为$ρ\frac{4}{3}π{R}^{3}$,根据万有引力定律有:
$F=\frac{G•ρ\frac{4}{3}π{R}^{3}•ρ\frac{4}{3}π{R}^{3}}{(2R)^{2}}=\frac{4G{ρ}^{2}{π}^{2}{R}^{4}}{9}$
由题意可知,当球体半径R减小时,两球间的万有引力将减小,故B正确,ACD错误.
故选:B.
点评 万有引力定律有应用,关键注意半径变化是两球质量随之变化,另两球间的距离亦发生变化,部分同学会考虑到质量的变化而忘了距离的变化而出错.

练习册系列答案
相关题目
15. 如图所示,一根细绳长L,一端固定一质量为M的小球,以另一端O为圆心,使小球在竖直面内做圆周运动.以下说法正确的是( )
如图所示,一根细绳长L,一端固定一质量为M的小球,以另一端O为圆心,使小球在竖直面内做圆周运动.以下说法正确的是( )
 如图所示,一根细绳长L,一端固定一质量为M的小球,以另一端O为圆心,使小球在竖直面内做圆周运动.以下说法正确的是( )
如图所示,一根细绳长L,一端固定一质量为M的小球,以另一端O为圆心,使小球在竖直面内做圆周运动.以下说法正确的是( )| A. | 小球过最高点时,绳子所受的弹力可以等于零 | |
| B. | 小球过最高点时的最小速度为0 | |
| C. | 小球过最高点时的最小速度为$\sqrt{gL}$ | |
| D. | 小球在最低点处于失重状态 |
19. 小车上有一根固定的水平横杆,横杆左端固定的斜杆与竖直方向成θ角,斜杆下端连接一质量为m的小铁球.横杆右端用一根轻质细线悬挂一相同的小铁球,当小车在水平面上做直线运动时,细线保持与竖直方向成α角(α≠θ),设斜杆对小铁球的作用力为F,下列说法正确的是( )
小车上有一根固定的水平横杆,横杆左端固定的斜杆与竖直方向成θ角,斜杆下端连接一质量为m的小铁球.横杆右端用一根轻质细线悬挂一相同的小铁球,当小车在水平面上做直线运动时,细线保持与竖直方向成α角(α≠θ),设斜杆对小铁球的作用力为F,下列说法正确的是( )
 小车上有一根固定的水平横杆,横杆左端固定的斜杆与竖直方向成θ角,斜杆下端连接一质量为m的小铁球.横杆右端用一根轻质细线悬挂一相同的小铁球,当小车在水平面上做直线运动时,细线保持与竖直方向成α角(α≠θ),设斜杆对小铁球的作用力为F,下列说法正确的是( )
小车上有一根固定的水平横杆,横杆左端固定的斜杆与竖直方向成θ角,斜杆下端连接一质量为m的小铁球.横杆右端用一根轻质细线悬挂一相同的小铁球,当小车在水平面上做直线运动时,细线保持与竖直方向成α角(α≠θ),设斜杆对小铁球的作用力为F,下列说法正确的是( )| A. | F沿斜杆向下,F=$\frac{mg}{cosθ}$ | B. | F沿斜杆向上,F=$\frac{mg}{cosα}$ | ||
| C. | F平行于细线向下,F=$\frac{mg}{cosθ}$ | D. | F平行于细线向上,F=$\frac{mg}{cosα}$ |
 如图所示,一个单匝矩形线圈水平放在桌面上,再线圈中心上方有一竖直的条形磁体,此时线圈内的磁通量为0.05Wb.在0.5s的时间内,将该条形磁体从图示位置竖放到线圈内的桌面上,此时线圈内的磁通量为0.10Wb.试求此过程:
如图所示,一个单匝矩形线圈水平放在桌面上,再线圈中心上方有一竖直的条形磁体,此时线圈内的磁通量为0.05Wb.在0.5s的时间内,将该条形磁体从图示位置竖放到线圈内的桌面上,此时线圈内的磁通量为0.10Wb.试求此过程: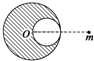 有一质量为M半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的质点,现在从M中挖去一半径为$\frac{R}{2}$的球体,如图所示,
有一质量为M半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的质点,现在从M中挖去一半径为$\frac{R}{2}$的球体,如图所示,