题目内容
1.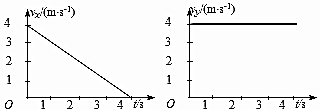 一物体在光滑水平面上运动,建立平面直角坐标系xOy,将物体的运动分解到x轴,y轴方向,其分速度vx和vy随时间变化的图线如图所示,求:
一物体在光滑水平面上运动,建立平面直角坐标系xOy,将物体的运动分解到x轴,y轴方向,其分速度vx和vy随时间变化的图线如图所示,求:(1)物体的初速度;
(2)物体在0-4s内的位移.
分析 (1)由图读出t=0s时x轴和y轴方向的分速度,合成求出物体的速度.
(2)物体在y轴方向做匀速直线运动,x轴方向做匀加速运动,分别求出两个方向的分位移,再合成求解物体的合位移.
解答 解:(1)t=0s时,vx=4m/s,vy=3m/s,则v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5m/s
tanθ=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{3}{4}$,θ=37°,即速度方向与x轴正方向成37°偏正y方向.
(2)t=4s时,y=vyt=16m,x=$\frac{1}{2}$at2=8m
故S=$\sqrt{{x}^{2}+{y}^{2}}$=8$\sqrt{5}$m,
tanα=$\frac{y}{x}$=$\frac{16}{8}$=2,
α=arctan2,即位移方向与速度方向与x轴正方向成arctan2偏正y方向.
答:(1)物体的初速度大小5m/s,与x轴正方向成37°偏正y方向;
(2)物体在0-4s内的位移大小8$\sqrt{5}$m,与x轴正方向成arctan2偏正y方向.
点评 本题是运动的合成问题,包括加速度、速度、位移的合成,都按平行四边形定则进行合成.

练习册系列答案
相关题目
11. 如图所示,一个大轮通过皮带拉着一个小轮转动,假设皮带和两轮之间没有打滑,而且R1=2R2,A为大轮边缘一点,B为小轮边缘一点,C为R1的中点,那么A、B、C三点的( )
如图所示,一个大轮通过皮带拉着一个小轮转动,假设皮带和两轮之间没有打滑,而且R1=2R2,A为大轮边缘一点,B为小轮边缘一点,C为R1的中点,那么A、B、C三点的( )
 如图所示,一个大轮通过皮带拉着一个小轮转动,假设皮带和两轮之间没有打滑,而且R1=2R2,A为大轮边缘一点,B为小轮边缘一点,C为R1的中点,那么A、B、C三点的( )
如图所示,一个大轮通过皮带拉着一个小轮转动,假设皮带和两轮之间没有打滑,而且R1=2R2,A为大轮边缘一点,B为小轮边缘一点,C为R1的中点,那么A、B、C三点的( )| A. | 线速度之比1:2:1 | B. | 角速度之比2:1:2 | ||
| C. | 向心加速度之比1:4:2 | D. | 以上均不正确 |
12. 一带正电的粒子从坐标原点O以一定的初速度v0沿电场中的x轴的正向做直线运动,x轴上的电势分布如图所示,则粒子从O点运动到x=x0的过程中,下列说法正确的是( )
一带正电的粒子从坐标原点O以一定的初速度v0沿电场中的x轴的正向做直线运动,x轴上的电势分布如图所示,则粒子从O点运动到x=x0的过程中,下列说法正确的是( )
 一带正电的粒子从坐标原点O以一定的初速度v0沿电场中的x轴的正向做直线运动,x轴上的电势分布如图所示,则粒子从O点运动到x=x0的过程中,下列说法正确的是( )
一带正电的粒子从坐标原点O以一定的初速度v0沿电场中的x轴的正向做直线运动,x轴上的电势分布如图所示,则粒子从O点运动到x=x0的过程中,下列说法正确的是( )| A. | 粒子的电势能先增大后减小 | |
| B. | 粒子的动能先增大后减小 | |
| C. | 粒子的加速度先增大后减小 | |
| D. | 粒子运动的电场力先沿x轴负方向后沿x轴正方向 |
9.在日本福岛核电站的核泄漏事故中,泄露的污染物中含有131I和137Cs两种放射性元素,它们通过一系列衰变产生对人体有危害的辐射,其中137I的衰变方程为${\;}_{53}^{131}$I→${\;}_{54}^{131}$Xe+${\;}_{-1}^{0}$e,其半衰期为8天,下列说法正确的是( )
| A. | 该核反应中放出的电子来自原子的外层电子 | |
| B. | ${\;}_{53}^{131}$I原子核中含有53个中子 | |
| C. | 因为该反应出现质量亏损,所以核反应后的原子核总质量数减少了 | |
| D. | 经过16天,75%的${\;}_{53}^{131}$I原子核发生了衰变 |
16.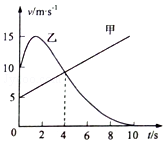 甲、乙两辆汽车沿同一方向做直线运动,两车在某一时刻刚好经过同一位置,此时甲的速度为5m/s,乙的速度为10m/s,以此时作为计时起点,它们的速度随时间变化的关系如图所示,根据以上条件可知( )
甲、乙两辆汽车沿同一方向做直线运动,两车在某一时刻刚好经过同一位置,此时甲的速度为5m/s,乙的速度为10m/s,以此时作为计时起点,它们的速度随时间变化的关系如图所示,根据以上条件可知( )
 甲、乙两辆汽车沿同一方向做直线运动,两车在某一时刻刚好经过同一位置,此时甲的速度为5m/s,乙的速度为10m/s,以此时作为计时起点,它们的速度随时间变化的关系如图所示,根据以上条件可知( )
甲、乙两辆汽车沿同一方向做直线运动,两车在某一时刻刚好经过同一位置,此时甲的速度为5m/s,乙的速度为10m/s,以此时作为计时起点,它们的速度随时间变化的关系如图所示,根据以上条件可知( )| A. | 在t=4s时,甲、乙两车相距最远 | |
| B. | 在t=10s时,乙车恰好回到出发点 | |
| C. | 乙车在运动过程中速度的方向发生改变 | |
| D. | 乙车做加速度先增大后减小的变加速运动 |
6.在人类对微观世界进行探索的过程中,科学实验起到了非常重要的作用,下列说法符合历史事实的是( )
| A. | 汤姆孙在α粒子散射实验中发现了电子 | |
| B. | 卢瑟福在原子核人工转变的实验中发现了中子 | |
| C. | 爱因斯坦为了解释光电效应的实验规律提出了光子说 | |
| D. | 贝克勒尔通过对天然放射现象的研究,发现了原子中存在的原子核 |
13.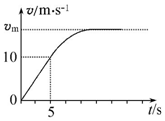 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率继续运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.2倍,g取10m/s2,则( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率继续运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.2倍,g取10m/s2,则( )
 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率继续运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.2倍,g取10m/s2,则( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率继续运动,其v-t图象如图所示.已知汽车的质量为m=2×103kg,汽车受到地面的阻力为车重的0.2倍,g取10m/s2,则( )| A. | 汽车在前5 s内的牵引力为4×103N | B. | 汽车在前5 s内的牵引力为8×103 N | ||
| C. | 汽车的额定功率为40kW | D. | 汽车的最大速度为20m/s |
6. 如图所示,质量为m、连长为l的正方形线框abcd,在竖直平面内从有水平边界的匀强磁场上方h高处由静止自由下落.线框电阻为R,磁场宽度为H(l<H),磁感应强度为B,线框竖直下落过程中,ab边始终与磁场边界平行.已知ab边进入磁场时和ab边穿出磁场时的速度相等.此过程中( )
如图所示,质量为m、连长为l的正方形线框abcd,在竖直平面内从有水平边界的匀强磁场上方h高处由静止自由下落.线框电阻为R,磁场宽度为H(l<H),磁感应强度为B,线框竖直下落过程中,ab边始终与磁场边界平行.已知ab边进入磁场时和ab边穿出磁场时的速度相等.此过程中( )
 如图所示,质量为m、连长为l的正方形线框abcd,在竖直平面内从有水平边界的匀强磁场上方h高处由静止自由下落.线框电阻为R,磁场宽度为H(l<H),磁感应强度为B,线框竖直下落过程中,ab边始终与磁场边界平行.已知ab边进入磁场时和ab边穿出磁场时的速度相等.此过程中( )
如图所示,质量为m、连长为l的正方形线框abcd,在竖直平面内从有水平边界的匀强磁场上方h高处由静止自由下落.线框电阻为R,磁场宽度为H(l<H),磁感应强度为B,线框竖直下落过程中,ab边始终与磁场边界平行.已知ab边进入磁场时和ab边穿出磁场时的速度相等.此过程中( )| A. | 线框的最大速度为$\frac{mgR}{{B}^{2}{l}^{2}}$ | |
| B. | 线框中产生的电热为mg(H-l) | |
| C. | 线框中通过的电荷量为$\frac{B{H}^{2}}{R}$ | |
| D. | ad边离开磁场的瞬间克服安培力做功的功率为$\frac{2{B}^{2}{l}^{2}g(h+l-H)}{R}$ |
7.下列说法正确的是( )
| A. | 发现中子的核反应方程是${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+${\;}_{0}^{1}$n | |
| B. | 20个${\;}_{92}^{238}$U原子核经过一个半衰期后,还有10个未发生衰变 | |
| C. | 一群处于n=4能级的氢原子向低能级跃迁,最多可释放出3种频率的光子 | |
| D. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是核衰变反应方程 |