题目内容
【题目】如图所示，P是倾角为30°的光滑固定斜面，劲度系数为k的轻弹簧一端圆定在斜面底端的固定板C上，另一段与质量为m的物块A相连接。细绳的一端系在物体A上，细绳跨过不计质量和摩擦的定滑轮，另一端有一个不计质量的小挂钩。小挂钩不任何物体时，物体A处于静止状态，细绳与斜面平行在小挂钩上轻轻挂上一个质量也为m的物块B后，物块A沿斜面向上运动。斜面是够长，动过程中B始终未接触地面，已知重力加速度为g求
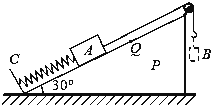
（1）物块A处于静止时，弹簧的压缩量；
（2）设物块A沿斜面上升通过Q点位置时速度最大，求Q点到出发点的距离X0和最大速度vm
（3）把物块B的质量变为原米的N倍（N>0.5），小明同学认为，只要N足够大，就可以使物块A沿斜面上滑到Q点时的速度增大到2vm，你认为是否正确?如果正确，请说明理由,如果不正确，请求出A沿斜面上升到Q点位置的速度的范围；
【答案】（1）
（2）
；
（3）
【解析】
（1）物块A处于静止状态时受力如图：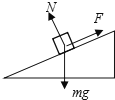
由平衡条件有：mgsin30°=k△x1
解得：△x1=
（2）A加速上升阶段，弹簧恢复原长前对A用牛顿第二定律有T+kx-mgsin30°=ma
对B由牛顿第二定律有mg-T=ma，
解得 mgsin30°+kx=2ma，
物体A在上升过程中，x减小，a减小，v增大；弹簧变为伸长后同理得mgsin30°-kx=2ma，上升过程x增大，a减小，v继续增大；可见，当kx=mgsin30°时a=0，速度达到最大．此时弹簧的伸长量 x=△x1
Q点速度最大，对应的弹力大小恰好是
，弹性势能和初始状态相同．故A上升到Q点过程，A、B的位移大小都是 x0=2△x1=
对A、B和弹簧系统用机械能守恒定律有
mg2△x1=mg2△x1sin30°+
2mvm2
可得 vm=g
（3）不正确；
由能的转化与守恒得：Nmg2△x1=mg2△x1sin30°+(Nm+m)v2
解得
，△x1=
当N=0.5时，v=0，当N→∞时，v=g
=2vm
故A沿斜面上升到Q点位置时的速度的范围是 0＜v＜g=2vm．
