题目内容
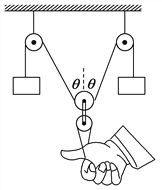
【题目】如图所示,原长分别为L1和L2劲度系数分别为k1和k2的轻质弹簧竖直地悬挂在天花板下.两弹簧之间有一个质量为m1的物体,最下端挂着质量为m2的另一物体.整个装置处于静止状态,这时两个弹簧长度为__________________.用一个质量为m的平板把下面的物体竖直地缓慢地向上托起,直到两个弹簧的总长度等于两弹簧的原长之和,这时平板受到下面物体的压力大小等于_________ .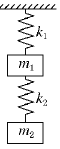
【答案】（1）
（2）
【解析】
（1）劲度系数为k1轻质弹簧受到的向下拉力（m1+m2）g，设它的伸长量为x1，根据胡克定律有：（m1+m2）g=k1 x1 （2分）
解得：
（2分）
劲度系数为k2轻质弹簧受到的向下拉力m2g，设它的伸长量为x2，根据胡克定律有：
m2g=k2 x2 （2分）
解得：
（2分）
这时两个弹簧的总长度为：L=L1+L2+x1+x2=L1+L2+
+
（2分）
（2）根据题意，下面的弹簧应被压缩x，上面的弹簧被拉伸x。
以m1为对象，根据平衡关系有 （k1+k2）x=m1g （2分）
解得：
（1分）
以m2为对象，设平板对m2的支持力为FN，根据平衡关系有
FN=k2x+m2g=
+m2g （2分）
故这时平板受到下面物体m2的压力FN＇=+m2g （1分）
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
