题目内容
7.在利用自由落体“验证机械能守恒定律”的实验中(图1),打点计时器所用电源频率为50Hz,当地重力加速度的值为9.8m/s2,测得所用重物的质量为1.00kg.若按实验要求正确地选出纸带进行测量,图中各个相邻的计数点间还有一个点没有画出来,测量得A、B、C三个计数点到第一个点O的距离如图2所示,单位均是cm,那么(计算结果均保留三位有效数字):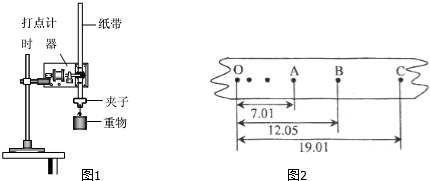
①纸带的左端与重物相连(填左或右);
②打点计时器打下计数点B时,物体的速度vB=1.50m/s
③从起点D到打下计数点B的过程中重力势能减少量是△Ep=1.18J,此过程中物体动能的增加量是△Ek=1.13J;
④通过计算,数值上△Ep>△Ek(填“>”“=”或“<”)
⑤实验的结论是在误差允许范围内,物体的机械能守恒.
分析 纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值,由于物体下落过程中存在摩擦阻力,因此动能的增加量小于势能的减小量.
解答 解:①从纸带上可以看出0点为打出来的第一个点,速度为0,重物自由下落,初速度为0,所以应该先打出0点,
而与重物相连的纸带在下端,应该先打点.所以纸带的P端应与重物相连.
②利用匀变速直线运动的推论
vB=$\frac{{x}_{AC}}{2T}$=$\frac{19.01-7.01}{4×0.02}×1{0}^{-2}$=1.5m/s
③重力势能减小量△Ep=mgh=1×9.8×0.1205J=1.18 J.
EkB=$\frac{1}{2}$mvB2=$\frac{1}{2}×1×1.{5}^{2}$=1.13 J.
④由于物体下落过程中存在摩擦阻力,这样验证的系统误差总是使重物的重力势能的减少量略大于动能的增加量;
⑤在误差允许范围内,物体的机械能守恒;
故答案为:①左;②1.50m/s;③1.18J,1.13J;④>;⑤在误差允许范围内,机械能守恒.
点评 要知道重物带动纸带下落过程中能量转化的过程和能量守恒,重物带动纸带下落过程中,除了重力还受到阻力,从能量转化的角度,由于阻力做功,重力势能减小除了转化给了动能还有一部分转化给摩擦产生的内能.

练习册系列答案
相关题目
9.关于电阻的计算式R=$\frac{U}{I}$和决定式R=ρ$\frac{L}{S}$,下面说法正确的是( )
| A. | 导体的电阻与电阻两端的电压成正比,与电流成反比 | |
| B. | 导体的电阻仅与导体长度、横截面积和材料有关 | |
| C. | 导体的电阻与工作温度无关 | |
| D. | 对于一定的导体来说,在恒温下比值$\frac{U}{I}$是恒定的,导体电阻不随U或I的变化而变化 |
10.一位4岁小男孩从高15层的楼顶坠下,被同楼的一位青年在楼下接住,幸免于难,设每层楼的高度为3m,这位青年从他所在的地方到楼下需要的时间是1.3s,则该青年要接住孩子,至多允许他反应的时间是(g=10m/s2)( )
| A. | 3.0s | B. | 1.7s | C. | 0.4s | D. | 1.3s |
7.甲乙两个物体在同一时刻沿同一直线运动,它们的速度-时间图象如图所示,下列有关说法正确的是( )


| A. | 在4~6 s内,甲、乙两物体的加速度大小相等,方向相反 | |
| B. | 甲、乙两物体一定在2 s末相遇 | |
| C. | 前4 s内甲、乙两物体的平均速度相等 | |
| D. | 前6 s内甲通过的路程更大 |
2.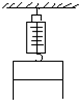 如图所示,封有空气的气缸挂在测力计上,测力计的示数为F,且已知气缸套的质量为M,活塞的质量为m、面积为S,气缸壁与活塞间摩擦不计,外界大气压强为p0,则气缸内空气的压强为( )
如图所示,封有空气的气缸挂在测力计上,测力计的示数为F,且已知气缸套的质量为M,活塞的质量为m、面积为S,气缸壁与活塞间摩擦不计,外界大气压强为p0,则气缸内空气的压强为( )
 如图所示,封有空气的气缸挂在测力计上,测力计的示数为F,且已知气缸套的质量为M,活塞的质量为m、面积为S,气缸壁与活塞间摩擦不计,外界大气压强为p0,则气缸内空气的压强为( )
如图所示,封有空气的气缸挂在测力计上,测力计的示数为F,且已知气缸套的质量为M,活塞的质量为m、面积为S,气缸壁与活塞间摩擦不计,外界大气压强为p0,则气缸内空气的压强为( )| A. | p0-$\frac{Mg}{s}$ | B. | p0+$\frac{(Mg-F)}{S}$ | C. | p0-$\frac{[F-(m+M)g]}{S}$ | D. | p0-$\frac{mg}{s}$ |
12.将30Ω的电阻接在一电源两端,通过的电流为0.3A.若把30Ω的电阻拿走,将10Ω与60Ω的电阻分别接在这个电源两端(电源内阻不计),那么通过的电流分别为( )
| A. | 0.9A,0.15A | B. | 0.15A,0.9A | C. | 0.1A,0.6A | D. | 0.6A,0.1A |
16.把阻值为5Ω、5Ω、10Ω的三个电阻任意连接,得到的等效电阻的阻值( )
| A. | 在5Ω到10Ω之间 | B. | 在2Ω到10Ω之间 | C. | 小于2Ω | D. | 大于20Ω |
17.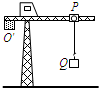 如图所示,塔吊臂上有一小车P,小车P吊着一个质量为m的货物Q.若小车P将货物Q 以加速度大小a竖直向上匀加速吊起,重力加速度为g,则在货物Q上升了h高度的过程中,重力、拉力对货物Q所做的功分别为( )
如图所示,塔吊臂上有一小车P,小车P吊着一个质量为m的货物Q.若小车P将货物Q 以加速度大小a竖直向上匀加速吊起,重力加速度为g,则在货物Q上升了h高度的过程中,重力、拉力对货物Q所做的功分别为( )
 如图所示,塔吊臂上有一小车P,小车P吊着一个质量为m的货物Q.若小车P将货物Q 以加速度大小a竖直向上匀加速吊起,重力加速度为g,则在货物Q上升了h高度的过程中,重力、拉力对货物Q所做的功分别为( )
如图所示,塔吊臂上有一小车P,小车P吊着一个质量为m的货物Q.若小车P将货物Q 以加速度大小a竖直向上匀加速吊起,重力加速度为g,则在货物Q上升了h高度的过程中,重力、拉力对货物Q所做的功分别为( )| A. | mgh,mah | B. | -mgh,mgh | C. | -mgh,m(g+a)h | D. | -mgh,m(g-a)h |
