题目内容
如图所示,从地面上A点发射一枚远程弹道导弹,在引力作用下,沿ACB椭圆轨道飞行击中地面目标B,C为轨道的远地点,距地面高度为h.已知地球半径为R,地球质量为M,引力常量为G.设距地面高度为h的圆轨道上卫星运动周期为T0.下列结论正确的是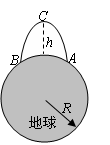
A.导弹在C点的速度大于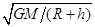 |
B.导弹在C点的加速度等于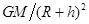 |
| C.地球球心为导弹椭圆轨道的一个焦点 |
| D.导弹从A点运动到B点的时间一定小于T0 |
BCD
解析试题分析:若在C点做匀速圆周运动的速度等于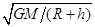 ,因为做椭圆运动,在C点提供的力大于所需要的向心力,所以导弹在C点的速度小于
,因为做椭圆运动,在C点提供的力大于所需要的向心力,所以导弹在C点的速度小于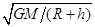 ,故A错;导弹在C点受到的万有引力,导弹在C点的加速度等于
,故A错;导弹在C点受到的万有引力,导弹在C点的加速度等于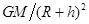 ,故B正确;导弹做的是椭圆运动,地球位于椭圆的焦点上.故C正确;根据开普勒第三定律,椭圆轨道的半长轴小于圆轨道的半径,所以椭圆的周期小于圆的周期,所以导弹从点A运动到B点的时间一定小于T0.故D正确.
,故B正确;导弹做的是椭圆运动,地球位于椭圆的焦点上.故C正确;根据开普勒第三定律,椭圆轨道的半长轴小于圆轨道的半径,所以椭圆的周期小于圆的周期,所以导弹从点A运动到B点的时间一定小于T0.故D正确.
考点:万有引力定律及其应用;人造卫星的加速度、周期和轨道的关系。

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案一飞船在某行星表面附近沿圆轨道绕该行星飞行.认为行星是密度均匀的球体.要确定该行星的密度,只需要测量( )
| A.飞船的轨道半径 | B.飞船的运行速度 |
| C.飞船的运行周期 | D.行星的质量 |
我国“嫦娥一号”探月卫星发射后,先在“24小时轨道”上绕地球运行(即绕地球一圈需要24小时);然后,经过两次变轨依次到达“48小时轨道”和“72小时轨道”;最后奔向月球.如果按圆形轨道计算,并忽略卫星质量的变化,则在每次变轨完成后与变轨前相比,( )
| A.卫星绕行速度变大 |
| B.卫星所受向心力增大 |
| C.卫星的机械能守恒 |
| D.卫星动能减小,引力势能增大 |
关于所有的地球同步卫星,下列说法正确的是
| A.向心力相同 | B.周期相同 |
| C.向心加速度相同 | D.离地心的距离相同 |
经国际小行星命名委员会命名的“神舟星”和“杨利伟星”的轨道均处在火星和木星轨道之间,它们绕太阳沿椭圆轨道运行,其轨道参数如下表。
| | 远日点 | 近日点 |
| 神舟星 | 3.575AU | 2.794AU |
| 杨利伟星 | 2.197AU | 1.649AU |
“神舟星”和“杨利伟星”绕太阳运行的周期分别为T1和T2,它们在近日点的加速度分别为a1和a2。则下列说法正确的是
A.
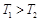 ,
,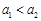 B.
B.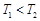 ,
,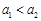
C.
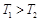 ,
,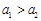 D.
D.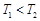 ,
,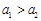
质量为m的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知月球质量为M,月球半径为R,月球表面重力加速度为g,引力常量为G,不考虑月球自转的影响,则航天器的
A.线速度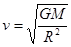 |
B.角速度为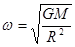 |
C.运行周期为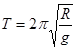 |
D.向心加速度为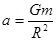 |
人造地球卫星的第一宇宙速度约为8 km/s,某行星的质量是地球质量的6倍,半径是地球半径的1.5倍.该行星上的第一宇宙速度约为
| A.16 km/s | B.32 km/s | C.46 km/s | D.2 km/s |







