题目内容
若假定“神舟九号”飞船绕地球做匀速圆周运动，它离地球表面的高度为h，运行周期为T，地球的半径为R，自转周期为T0，由此可推知地球的第一宇宙速度为（ ）
A． | B． |
C． | D． |
B
解析试题分析：由于T0是自转周期，不是卫星在地球表面附近的匀速圆周运动的周期，所以A选项错误；由于神舟九号”飞船绕地球做匀速圆周运动，由
， 
,解得
，联立两式解得
所以B选项正确，C选项错误；D选项中的轨道半径是R不是（R+h）,所以D选项错误。
考点：万有引力定律 匀速圆周运动 周期 线速度 第一宇宙速度
一物体在地球表面上的重力为16N，它在以5m/s2的加速度加速上升的火箭中的示重9N，g=10m/s2，则此时火箭离地面的高度是地球半径R的：
| A．2倍 | B．3倍 | C．4倍 | D．0.5倍 |
“嫦娥三号”探月工程将在今年下半年完成．假设月球半径为
，月球表面的重力加速度为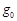
．飞船沿距月球表面高度为3的圆形轨道Ⅰ运动，到达轨道的
点，点火变轨进入椭圆轨道Ⅱ，到达轨道Ⅱ的近月点
再次点火进入近月轨道Ⅲ绕月球做圆周运动．下列判断正确的是
A．飞船在轨道Ⅲ上的运行速率 |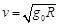
B．飞船在轨道Ⅰ绕月球运动一周所需的时间为 |
| C．飞船在点点火变轨后，动能增大 |
| D．飞船在Ⅱ轨道上由A点运动到B点的过程中，动能增大 |
如图所示，从地面上A点发射一枚远程弹道导弹，在引力作用下，沿ACB椭圆轨道飞行击中地面目标B，C为轨道的远地点，距地面高度为h．已知地球半径为R，地球质量为M，引力常量为G．设距地面高度为h的圆轨道上卫星运动周期为T0．下列结论正确的是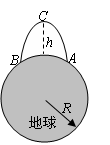
A．导弹在C点的速度大于 |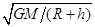
B．导弹在C点的加速度等于 |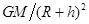
| C．地球球心为导弹椭圆轨道的一个焦点 |
| D．导弹从A点运动到B点的时间一定小于T0 |
“嫦娥一号”于2009年3月1日成功发射，从发射到撞月历时433天，其中，卫星先在近地圆轨道绕行3周，再经过几次变轨进入近月圆轨道绕月飞行。若月球表面的自由落体加速度为地球表面的1/6，月球半径为地球的1/4，则根据以上数据对两个近地面轨道运行状况分析可得
| A．绕月与绕地飞行周期之比为3/2 |
| B．绕月与绕地飞行周期之比为2/3 |
| C．绕月与绕地飞行向心加速度之比为1/6 |
| D．月球与地球质量之比为1/96 |
2011年11月3日，我国发射的“天宫一号”目标飞行器与发射的“神舟八号”飞船成功进行了第一次无人交会对接。假设对接前“天宫一号”和“神舟八号”绕地球做匀速圆周运动的轨道如图所示，虚线A代表“天宫一号”的轨道，虚线B代表“神舟八号”的轨道，由此可以判断（ ）
| A．“天宫一号”的运行速率小于“神舟八号”的运行速率 |
| B．“天宫一号”和“神舟八号”的运行速率均大于第一宇宙速度 |
| C．“天宫一号”的周期小于“神舟八号”的周期 |
| D．“天宫一号”的向心加速度大于“神舟八号”的向心加速度 |
2010年10月1日18时59分57秒，我国在西昌卫星发射中心用“长征三号丙”运载火箭将“嫦娥二号”卫星成功送入太空．已知地球自转周期 T0，月球半径R，卫星距离月球表面的高度h，月球表面的重力加速度g，万有引力常量G.下列说法中正确的是( )
A．月球的质量M＝ |
B．卫星的角速度与地球自转的角速度之比为 |
C．月球的密度ρ＝ |
D．卫星绕月球运行的速率v＝ |
在圆轨道上运动的质量为m的人造地球卫星，它到地面的距离等于地球半径R，地面上的重力加速度为g，则
A．卫星运动的速度为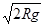 | B．卫星运动的周期为 |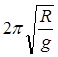
| C．卫星运动的加速度为g/2 | D．卫星的动能为mgR/4 |
甲、乙两颗人造卫星都绕地球做匀速圆周运动，甲为地球同步卫星，乙为近地卫星。关于这两颗卫星，下列说法中正确的是
| A．甲的运行速度一定大于乙的运行速度 |
| B．甲的运行周期一定大于乙的运行周期 |
| C．甲卫星在运行时不可能经过北京的正上方 |
| D．两卫星的运行速度均可以等于第一宇宙速度 |