题目内容
2. 如图所示,一玩溜冰的小孩(可视作质点)质量为m=30kg,他在左侧水平平台上滑行一段距离后平抛,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道.并沿轨道下滑,AB为圆弧两端点,其连线水平,已知从D点以v0=5m/s的速度向右滑行,经t=0.5s到达E点,圆弧半径为R=1.0m,对应圆心角为θ=106°,平台与AB连线的高度差为h=0.8m,小孩达到圆轨道O点时速度的大小为$\sqrt{33}$m/s(计算过程中取g=10m/s2,sin53°=0.8,cos53°=0.6).求:
如图所示,一玩溜冰的小孩(可视作质点)质量为m=30kg,他在左侧水平平台上滑行一段距离后平抛,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道.并沿轨道下滑,AB为圆弧两端点,其连线水平,已知从D点以v0=5m/s的速度向右滑行,经t=0.5s到达E点,圆弧半径为R=1.0m,对应圆心角为θ=106°,平台与AB连线的高度差为h=0.8m,小孩达到圆轨道O点时速度的大小为$\sqrt{33}$m/s(计算过程中取g=10m/s2,sin53°=0.8,cos53°=0.6).求:(1)小孩运动到圆弧轨道最低点O时对轨道的压力;
(2)小孩平抛的初速度和小孩溜冰与平台DE的摩擦因数.
分析 (1)在最低点,重力和支持力的合力提供圆周运动的向心力,根据向心力表达式求出支持力的大小,从而求出小孩对轨道的压力.
(2)由于小孩无碰撞进入圆弧轨道,即小孩落到A点时速度方向沿A点切线方向,根据平抛运动的基本公式及几何关系即可求解;
由运动学在DE段可求加速度,由牛顿第二定律可得摩擦因数.
解答 解:(1)在最低点,据牛顿第二定律,有:${F}_{N}-mg=m\frac{{{v}_{x}}^{2}}{R}$,
代入数据解得:FN=1290N
由牛顿第三定律可知,小孩对轨道的压力为1290N.
(2)由于小孩无碰撞进入圆弧轨道,即小孩落到A点时速度方向沿A点切线方向则:
则:tan 53?=$\frac{{v}_{y}}{{v}_{\;}}$,
又由:$h=\frac{1}{2}g{t}^{2}$,
得:$\sqrt{\frac{2h}{g}}$,
而:
vy=gt=10×0.4=4m/s
联立以上各式得:
v=3m/s.
由D到E的加速度为:
$a=\frac{v-{v}_{0}}{t}=\frac{3-5}{0.5}=-4m/{s}^{2}$,
由牛顿第二定律:
$a=\frac{-μmg}{m}=-μg$,
解得:
$μ=\frac{a}{-g}=\frac{-4}{-10}=0.4$.
答:
(1)小孩运动到圆弧轨道最低点O时对轨道的压力为1290N;
(2)小孩平抛的初速度为3m/s,小孩溜冰与平台DE的摩擦因数为0.4.
点评 解决本题的关键抓住无碰撞地从A进入,得出速度的方向.知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.以及知道知道在圆弧轨道的最低点,沿半径方向上的合力提供圆周运动的向心力

练习册系列答案
相关题目
7.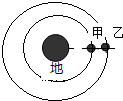 如图所示,甲乙两颗卫星绕地球做圆周运动,已知甲卫星的周期为N小时,每过9N小时,乙卫星都要运动到与甲卫星同居于地球一侧且三者共线的位置上,则甲、乙两颗卫星的线速度之比为( )
如图所示,甲乙两颗卫星绕地球做圆周运动,已知甲卫星的周期为N小时,每过9N小时,乙卫星都要运动到与甲卫星同居于地球一侧且三者共线的位置上,则甲、乙两颗卫星的线速度之比为( )
 如图所示,甲乙两颗卫星绕地球做圆周运动,已知甲卫星的周期为N小时,每过9N小时,乙卫星都要运动到与甲卫星同居于地球一侧且三者共线的位置上,则甲、乙两颗卫星的线速度之比为( )
如图所示,甲乙两颗卫星绕地球做圆周运动,已知甲卫星的周期为N小时,每过9N小时,乙卫星都要运动到与甲卫星同居于地球一侧且三者共线的位置上,则甲、乙两颗卫星的线速度之比为( )| A. | $\frac{\root{3}{9}}{2}$ | B. | $\frac{\root{3}{3}}{2}$ | C. | $\frac{2}{\root{3}{3}}$ | D. | $\frac{2}{\root{3}{9}}$ |
4. 如图所示,甲、乙两人在冰面上“拔河”.两人中间位置处有一分界线,约定先使对方过分界线者为赢.若绳子质量不计,冰面可看成光滑,则下列说法正确的是( )
如图所示,甲、乙两人在冰面上“拔河”.两人中间位置处有一分界线,约定先使对方过分界线者为赢.若绳子质量不计,冰面可看成光滑,则下列说法正确的是( )
 如图所示,甲、乙两人在冰面上“拔河”.两人中间位置处有一分界线,约定先使对方过分界线者为赢.若绳子质量不计,冰面可看成光滑,则下列说法正确的是( )
如图所示,甲、乙两人在冰面上“拔河”.两人中间位置处有一分界线,约定先使对方过分界线者为赢.若绳子质量不计,冰面可看成光滑,则下列说法正确的是( )| A. | 甲对绳的拉力与乙对绳的拉力是作用力与反作用力 | |
| B. | 甲对绳的拉力与绳对甲的拉力是一对平衡力 | |
| C. | 若乙的质量比甲小,则甲能赢得“拔河”比赛的胜利 | |
| D. | 若甲能赢得比赛的胜利,则甲对绳的拉力大于乙对绳的拉力 |
 如图所示,平行金属导轨ab、cd与水平面成θ角,间距为L,导轨与固定电阻R1和R2相连,磁感应强度为B的匀强磁场垂直穿过导轨平面.有一导体棒MN,质量为m,导体棒的电阻与固定电阻R1和R2的阻值均为R,与导轨之间的动摩擦因数为μ,导体棒以速度v沿导轨匀速下滑,忽略感应电流之间的作用.求:
如图所示,平行金属导轨ab、cd与水平面成θ角,间距为L,导轨与固定电阻R1和R2相连,磁感应强度为B的匀强磁场垂直穿过导轨平面.有一导体棒MN,质量为m,导体棒的电阻与固定电阻R1和R2的阻值均为R,与导轨之间的动摩擦因数为μ,导体棒以速度v沿导轨匀速下滑,忽略感应电流之间的作用.求: 一同学做飞镖游戏,已知圆盘的直径为d,飞镖距圆盘为L,且对准圆盘上边缘的A点水平抛出,初速度为v0,飞镖抛出的同时,圆盘以垂直圆盘且过盘心O的水平轴匀速转动,角速度为ω,若飞镖恰好击中A点,则圆盘转动的角速度ω1应满足什么条件?
一同学做飞镖游戏,已知圆盘的直径为d,飞镖距圆盘为L,且对准圆盘上边缘的A点水平抛出,初速度为v0,飞镖抛出的同时,圆盘以垂直圆盘且过盘心O的水平轴匀速转动,角速度为ω,若飞镖恰好击中A点,则圆盘转动的角速度ω1应满足什么条件? 一同学在离地某一高度处将一质量为m的小球以初速度v0竖直向上抛出,小球在空中运动过程中受到空气阻力f的作用,且满足f=kv,其中k为未知比例系数,v是小球运动的速率,该速率随时间的变化规律如图所示,经过时间t1,小球上升到最高点,然后再下落,回到抛出点时的速率为v1,且回到抛出点前小球已经做匀速运动,重力加速度为g,求:
一同学在离地某一高度处将一质量为m的小球以初速度v0竖直向上抛出,小球在空中运动过程中受到空气阻力f的作用,且满足f=kv,其中k为未知比例系数,v是小球运动的速率,该速率随时间的变化规律如图所示,经过时间t1,小球上升到最高点,然后再下落,回到抛出点时的速率为v1,且回到抛出点前小球已经做匀速运动,重力加速度为g,求: 如图为一列简谐波在t1=0时刻的图象.此时波中质点M的运动方向沿y负方向,且到t2=0.55s质点M恰好第3次到达y正方向最大位移处.试求:
如图为一列简谐波在t1=0时刻的图象.此时波中质点M的运动方向沿y负方向,且到t2=0.55s质点M恰好第3次到达y正方向最大位移处.试求: