题目内容
1.“嫦娥一号”探月卫星,2007年11月5日进入月球轨道后,经历3次轨道调整,进入工作轨道.若该卫星在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )| A. | 月球表面处的重力加速度g月为 $\frac{G_2}{G_1}g$ | |
| B. | 月球的质量与地球的质量之比为$\frac{{{G_1}R_2^2}}{{{G_2}R_1^2}}$ | |
| C. | 卫星在距月球表面轨道上做匀速圆周运动的周期T月为2π$\sqrt{\frac{{{R_2}{G_1}}}{{g{G_2}}}}$ | |
| D. | 月球的第一宇宙速度与地球的第一宇宙速度之比为$\sqrt{\frac{{{G_1}{R_2}}}{{{G_2}{R_1}}}}$ |
分析 A、根据卫星在地球表面和月球表面的重力之比知重力加速度之比,从而求出月球表面的重力加速度.
B、根据万有引力等于重力G$\frac{Mm}{{R}^{2}}$=mg,求出月球和地球的质量之比.
C、根据mg月=mR2($\frac{2π}{{T}_{月}}$)2,求出卫星在月球表面轨道上做匀速圆周运动的周期.
D、根据mg=m$\frac{{v}^{2}}{R}$,求出月球和地球的第一宇宙速度之比.
解答 解:A、卫星在地球表面的重力为G1,在月球表面的重力为G2,则 $\frac{{g}_{月}}{g}$=$\frac{{G}_{2}}{{G}_{1}}$,所以g月=$\frac{G_2}{G_1}g$.故A正确.
B、根据万有引力等于重力,有 G$\frac{Mm}{{R}^{2}}$=mg,知M=$\frac{g{R}^{2}}{G}$.中心天体的质量与半径和表面的重力加速度有关.所以月球的质量和地球的质量之比为 $\frac{{M}_{月}}{{M}_{地}}$=$\frac{{g}_{月}}{g}$•$\frac{{R}_{2}^{2}}{{R}_{1}^{2}}$=$\frac{{G}_{2}{R}_{2}^{2}}{{G}_{1}{R}_{1}^{2}}$.故B错误.
C、根据mg月=mR2($\frac{2π}{{T}_{月}}$)2,得T月=2π $\sqrt{\frac{{R}_{2}}{{g}_{月}}}$,而g月=$\frac{G_2}{G_1}g$,所以T月=2π$\sqrt{\frac{{{R_2}{G_1}}}{{g{G_2}}}}$.故C正确.
D、根据mg=m$\frac{{v}^{2}}{R}$,知第一宇宙速度v=$\sqrt{gR}$,而$\frac{{g}_{月}}{g}$=$\frac{{G}_{2}}{{G}_{1}}$,所以第一宇宙速度之比为 $\frac{{v}_{月}}{{v}_{地}}$=$\sqrt{\frac{{G}_{2}{R}_{2}}{{G}_{1}{R}_{1}}}$.故D错误.
故选:AC
点评 解决本题的关键掌握万有引力等于重力,知道卫星在月球表面轨道做圆周运动,靠重力提供向心力.

 发散思维新课堂系列答案
发散思维新课堂系列答案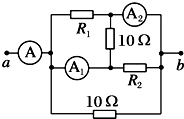
| A. | R1<R2,表A的读数为3.2 A | B. | R1>R2,表A的读数为3.2 A | ||
| C. | R1=R2,表A的读数为4 A | D. | R1>R2,表A的读数无法判断 |
| A. | 12.5 km/h | B. | 25 km/h | C. | 31.25 km/h | D. | 35 km/h |
 如图所示,是一位晨练者每天早晨进行锻炼时的行走路线,从A点出发,沿半径分别为3m和5m的半圆经B点到达C点,则他的位移和路程分别为( )
如图所示,是一位晨练者每天早晨进行锻炼时的行走路线,从A点出发,沿半径分别为3m和5m的半圆经B点到达C点,则他的位移和路程分别为( )| A. | 16m,方向从A到C;16m | B. | 16m,方向从A到C;25.1m | ||
| C. | 25.1m,方向从C到A;16m | D. | 25.1m,方向从A到C;16m |
| A. |  奥斯特通过如图所示实验发现了电磁感应现象 | |
| B. |  库仑通过如图所示装置测定了万有引力常量 | |
| C. |  安培通过如图所示实验发现了电流的磁效应 | |
| D. |  密立根通过如图所示的实验精确测定了电子的电荷量 |
 如图所示,倒置的光滑圆锥面内侧,有质量相同的两个小球A、B沿锥面在水平面内做匀速圆周运动.下列关于A、B两球的角速度、线速度和向心加速度的说法中,正确的是( )
如图所示,倒置的光滑圆锥面内侧,有质量相同的两个小球A、B沿锥面在水平面内做匀速圆周运动.下列关于A、B两球的角速度、线速度和向心加速度的说法中,正确的是( )| A. | 它们的周期相等 | B. | 它们的向心加速度相等 | ||
| C. | 它们的角速度A比B小 | D. | 它们的线速度A比B小 |
 一斜面AB长为9m,倾角为37°,一质量为2kg的小物体(大小不计)从斜面顶端A点由静止开始下滑,如图所示(sin37°=0.6 cos37°=0.8 g取10m/s2)
一斜面AB长为9m,倾角为37°,一质量为2kg的小物体(大小不计)从斜面顶端A点由静止开始下滑,如图所示(sin37°=0.6 cos37°=0.8 g取10m/s2)