题目内容
14.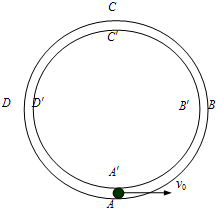 如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD光滑,内圆A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,已知圆形轨道的半径R=0.32m,取g=10m/s2.
如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD光滑,内圆A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,已知圆形轨道的半径R=0.32m,取g=10m/s2.(1)若要使小球始终紧贴外圆做完整的圆周运动,初速度v0至少为多少?
(2)若v0=3.8m/s,经过一段时间小球到达最高点,内轨道对小球的支持力F=2N,则小球在这段时间内克服摩擦力做的功是多少?
(3)若v0=3.9m/s,经过足够长的时间后,小球经过最低点A时受到的支持力为多少?小球在整个运动过程中减少的机械能是多少?
分析 (1)紧贴外圆做圆周运动,在最高点的临界情况是重力提供向心力,根据牛顿第二定律结合机械能守恒定律求出初速度的最小值.
(2)根据牛顿第二定律求出最高点的速度大小,根据动能定理求出克服摩擦力做功的大小.
(3)经足够长时间后,小球在下半圆轨道内做往复运动,根据动能定理和牛顿第二定律求出最低点小球所受的支持力大小,根据能量守恒求出损失的机械能.
解答 解:(1)设此情形下小球到达最高点的最小速度为vC,则有
mg=m$\frac{{v}_{C}^{2}}{R}$
根据机械能守恒得:$\frac{1}{2}m{v}_{0}^{2}$=$\frac{1}{2}m{v}_{C}^{2}$+2mgR
代入数据解得 v0=4m/s
(2)设此时小球到达最高点的速度为v′C,克服摩擦力做的功为W,则
mg-F=m$\frac{v{′}_{C}^{2}}{R}$
由动能定理得:
-2mgR-W=$\frac{1}{2}mv{′}_{C}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
代入数据解得 W=0.164J
(3)经足够长时间后,小球在下半圆轨道内做往复运动,设小球经过最低点的速度为vA,受到的支持力为NA,则有
mgR=$\frac{1}{2}m{v}_{A}^{2}$
由牛顿第二定律得:
NA-mg=m$\frac{{v}_{A}^{2}}{R}$
代入数据解得 NA=6N
设小球在整个运动过程中减少的机械能为△E,由功能关系有
△E=$\frac{1}{2}m{v}_{0}^{2}$-mgR
代入数据解得△E=0.881J
答:
(1)要使小球始终紧贴外圆做完整的圆周运动,初速度v0至少为4m/s.
(2)小球在这段时间内克服摩擦力做的功是0.164J.
(3)小球经过最低点A时受到的支持力为6N,小球在整个运动过程中减少的机械能是0.881J.
点评 本题综合考查了动能定理、牛顿第二定律和机械能守恒定律,综合性较强,关键是理清运动过程,抓住临界状态,运用合适的规律进行求解.

| A. | 61.0mm 65.8mm 70.7mm | B. | 41.2mm 45.1mm 53.0mm | ||
| C. | 49.6mm 53.5mm 57.3mm | D. | 60.5mm 61.0mm 60.6mm |
| A. | 第一宇宙速度与地球的质量有关 | |
| B. | 被发射的物体质量越大,第一宇宙速度越大 | |
| C. | 被发射的物体质量越小,第一宇宙速度越大 | |
| D. | 第一宇宙速度与被发射物体的质量无关 |
 如图所示,匀强磁场方向垂直于线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场,第一次速度v1=v,第二次速度v2=2v,在先、后两次过程中,正确的是( )
如图所示,匀强磁场方向垂直于线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场,第一次速度v1=v,第二次速度v2=2v,在先、后两次过程中,正确的是( )| A. | 线框中感应电流之比为1:2 | |
| B. | 线框中产生热量之比为1:2 | |
| C. | 沿运动方向作用在线框上的外力的功率之比为1:2 | |
| D. | 通过线圈横截面的电荷量之比1:2 |
 A、B小球在一条竖直线上,相聚H=10m,A、B、C三个小球同时以相同速率向不同的方向抛出,A竖直向下抛,B竖直向上抛,C想A、B所在的竖直线平抛,经0.5s三个球在空中相遇,g=10m/s2.求:
A、B小球在一条竖直线上,相聚H=10m,A、B、C三个小球同时以相同速率向不同的方向抛出,A竖直向下抛,B竖直向上抛,C想A、B所在的竖直线平抛,经0.5s三个球在空中相遇,g=10m/s2.求: 如图所示是弹簧振子的振动图象,从图象中可以看出:振子的振幅是10cm、频率是25 Hz.振子在4s内通过的路程是40m,该简谐运动的表达式为y=10sin50πt(cm).
如图所示是弹簧振子的振动图象,从图象中可以看出:振子的振幅是10cm、频率是25 Hz.振子在4s内通过的路程是40m,该简谐运动的表达式为y=10sin50πt(cm).
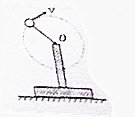 如图所示,长为L=1m的轻质木材,一端固定一个质量m=2kg的小球,以支架上的O点为轴在竖直面内做圆周运动,支架质量M=5kg,当小球运动到最高点时v=2m/s,则此时支架对地面的压力为多少?若要使支架对地面的压力为零,则小球运动到最高点时速度又该为多少?(g取10m/s2)
如图所示,长为L=1m的轻质木材,一端固定一个质量m=2kg的小球,以支架上的O点为轴在竖直面内做圆周运动,支架质量M=5kg,当小球运动到最高点时v=2m/s,则此时支架对地面的压力为多少?若要使支架对地面的压力为零,则小球运动到最高点时速度又该为多少?(g取10m/s2)