题目内容
13.用一台额定功率为P0=60kW的起重机,将一质量为m=500kg的工件由地面竖直向上吊起,不计摩擦等阻力,取g=10m/s2.求:(1)工件在被吊起的过程中所能达到的最大速度vm;
(2)若使工件以a=2m/s2的加速度从静止开始匀加速向上吊起,则匀加速过程能维持多长时间?
(3)若起重机在始终保持额定功率的情况下从静止开始吊起工件,经过t=1.14s工件的速度vt=10m/s,则此时工件离地面的高度h为多少?
分析 (1)当拉力等于重物重力时,重物的速度达到最大,结合功率与牵引力的关系以及拉力等于重力求出重物的最大速度;
(2)根据牛顿第二定律求出匀加速直线运动时的拉力大小,从而抓住匀加速直线运动结束功率达到额定功率求出匀加速直线运动的末速度,结合速度时间公式求出匀加速直线运动的时间;
(3)根据动能定理即可求解速度达到vt=10m/s时工件离地面的高度.
解答 解:(1)当工件达到最大速度时有:F=mg,P=P0=60kW
故有:vm=$\frac{{P}_{0}}{mg}$=$\frac{60000}{5000}$=12m/s;
(2)工件被匀加速向上吊起时,a不变,v变大,P也变大,当P=P0时匀加速过程结束,
根据牛顿第二定律得:F-mg=ma,
解得:F=m(a+g)=500×(2+10)N=6000N
匀加速过程结束时工件的速度为:v=$\frac{{P}_{0}}{F}$=$\frac{60000}{6000}$=10m/s,
匀加速过程持续的时间为:t0=$\frac{v}{a}$=$\frac{10}{2}$=5s;
(3)根据动能定理有:P0t-mgh=$\frac{1}{2}$mvt2-0
代入数据解得:h=8.68m.
答:(1)工件在被吊起的过程中所能达到的最大速度为12m/s;
(2)若使工件以a=2m/s2的加速度从静止开始匀加速向上吊起,则匀加速过程能维持5s;
(3)若起重机在始终保持额定功率的情况下从静止开始吊起工件,经过t=1.14s工件的速度vt=10m/s,则此时工件离地面的高度h为8.68m.
点评 解决本题的关键知道拉力等于重力时速度最大,匀加速直线运动结束,功率达到额定功率,结合牛顿第二定律以及功率与牵引力的关系进行求解.

练习册系列答案
相关题目
3.如图所示,A、B是一条电场线上的两点,可判定( )


| A. | 该电场可能是匀强电场 | |
| B. | A点的电势一定低于B点的电势 | |
| C. | 负电荷放在B点的电势能比A点的电势能大 | |
| D. | 负电荷放在B点所受电场力方向向右 |
4. 一辆车由甲地出发,沿平直公路开到乙地刚好停止,其速度图象如图所示,那么0~t和t~3t两段时间内,下列说法正确的是( )
一辆车由甲地出发,沿平直公路开到乙地刚好停止,其速度图象如图所示,那么0~t和t~3t两段时间内,下列说法正确的是( )
 一辆车由甲地出发,沿平直公路开到乙地刚好停止,其速度图象如图所示,那么0~t和t~3t两段时间内,下列说法正确的是( )
一辆车由甲地出发,沿平直公路开到乙地刚好停止,其速度图象如图所示,那么0~t和t~3t两段时间内,下列说法正确的是( )| A. | 加速度大小之比为1:2 | B. | 位移大小之比为1:2 | ||
| C. | 平均速度大小之比为2:1 | D. | 以上说法都不对 |
1.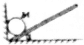 如图所示,一个质量为M的球靠墙置于水平光滑板上,墙也是光滑的,当平板的一端慢慢抬起,使之与水平方向的夹角由0°变为α,在此过程中,墙受的压力大小的变化情况是变大;平板受到的压力大小变化情况是变大.
如图所示,一个质量为M的球靠墙置于水平光滑板上,墙也是光滑的,当平板的一端慢慢抬起,使之与水平方向的夹角由0°变为α,在此过程中,墙受的压力大小的变化情况是变大;平板受到的压力大小变化情况是变大.
 如图所示,一个质量为M的球靠墙置于水平光滑板上,墙也是光滑的,当平板的一端慢慢抬起,使之与水平方向的夹角由0°变为α,在此过程中,墙受的压力大小的变化情况是变大;平板受到的压力大小变化情况是变大.
如图所示,一个质量为M的球靠墙置于水平光滑板上,墙也是光滑的,当平板的一端慢慢抬起,使之与水平方向的夹角由0°变为α,在此过程中,墙受的压力大小的变化情况是变大;平板受到的压力大小变化情况是变大.
18.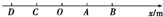 某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
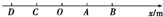 某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )| A. | 质点在A→B→C的时间内发生的位移为2 m,方向沿x轴正方向,路程为4 m | |
| B. | 质点在B→D的时间内发生的位移为-4 m,方向沿x轴负方向,路程为4 m | |
| C. | 当质点到达D点时,其位置可用D点的坐标-2 m表示 | |
| D. | 当质点到达D点时,相对于A点的位移为-3 m |
14.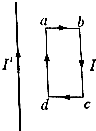 长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
 长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )| A. | 线框的ab和cd边不受安培力 | |
| B. | 线框所受的安培力合力向右 | |
| C. | 线框所受的安培力合力向左 | |
| D. | 若长直导线的电流I′加倍,则稳定后线框所受的安培力合力也随之加倍 |
15. 如图所示,一直流电动机与阻值R=9Ω的电阻串联在电路上,电动势E=30V,内阻r=1Ω,用理想电压表测出电动机两端电压U=10V,已知电动机线圈电阻RM=1Ω,下列说法中正确的是( )
如图所示,一直流电动机与阻值R=9Ω的电阻串联在电路上,电动势E=30V,内阻r=1Ω,用理想电压表测出电动机两端电压U=10V,已知电动机线圈电阻RM=1Ω,下列说法中正确的是( )
 如图所示,一直流电动机与阻值R=9Ω的电阻串联在电路上,电动势E=30V,内阻r=1Ω,用理想电压表测出电动机两端电压U=10V,已知电动机线圈电阻RM=1Ω,下列说法中正确的是( )
如图所示,一直流电动机与阻值R=9Ω的电阻串联在电路上,电动势E=30V,内阻r=1Ω,用理想电压表测出电动机两端电压U=10V,已知电动机线圈电阻RM=1Ω,下列说法中正确的是( )| A. | 通过电动机的电流为10 A | B. | 通过电动机的电流小于10 A | ||
| C. | 电动机的输出功率大于16 W | D. | 电动机的输出功率小于16 W |
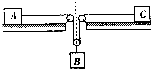 如图所示,半径为R的水平转台中央有一个小孔,水平转台可绕小孔中心轴匀速转动,物块A、C置于转台的边缘,物块A、C的质量均为m,随转台一起转动,用细绳通过大小不计的轻质滑轮悬挂物块B,三物块均可看成质点.已知物块A、C与转台间的动摩擦因数均为μ=0.5,水平转台的角速度ω=$\sqrt{\frac{2μg}{R}}$,重力加速度大小为g.要使物块B静止不动,物块A、B的质量之比可能为( )
如图所示,半径为R的水平转台中央有一个小孔,水平转台可绕小孔中心轴匀速转动,物块A、C置于转台的边缘,物块A、C的质量均为m,随转台一起转动,用细绳通过大小不计的轻质滑轮悬挂物块B,三物块均可看成质点.已知物块A、C与转台间的动摩擦因数均为μ=0.5,水平转台的角速度ω=$\sqrt{\frac{2μg}{R}}$,重力加速度大小为g.要使物块B静止不动,物块A、B的质量之比可能为( )