题目内容
3.一列队伍长L=120m,行进速度v1=1.6m/s,为了传达一个命令,通讯员从队伍排尾跑步赶到队伍排头,其速度v2=3m/s,然后又立即用与队伍行进速度相同大小的速度返回排尾,问:(1)通讯员从离开队尾到重又回到队尾共需多少时间?
(2)通讯员回到队尾处与离开队尾处相距多远?
分析 通讯员和行进中的队伍,两者都作匀速直线运动,其运动示意图如图所示.设队伍原位置为AB,通讯员从排尾赶到排头时,排头已到位置A',所用时间为t,通讯员返回排尾时,排头的位置为A″,所用时间为t′.在时间t内,通讯员与队伍位移之差等于L;在时间t′内,通讯员与队伍位移大小之和等于L.
解答 解:(1)通讯员从排尾赶到排头时,有关系式:
v2t-v1t=L…①
设通讯员从排头返回排尾的速度为v2′,其值为v2′=v1=1.6m/s,又有关系式:
v1t'+v'2t'=2v1t'=L…②
联立两式,得通讯员从离开队伍(排尾)到重新返回排尾共需时间:T=t+t′=$\frac{L}{{v}_{2}-{v}_{1}}$+$\frac{L}{2{v}_{1}}$=$\frac{{v}_{1}+{v}_{2}}{2{v}_{1}({v}_{2}-{v}_{1})}L$=$\frac{1.6+3}{2×1.6×(3-1.6)}$×120=123s;
(2)通讯员归队处与离队处相隔距离就是整个队伍在同样时间内行进的距离,即:
s'=v1T=1.6×123.2m=197.1m
答:(1)通讯员从离开队伍到重又回到排尾共需时间 123s
(2)通讯员归队处与离队处相距197.1m
点评 解决此类题目主要是要理清相对速度关系和相对位移关系.无论是从排头跑步到队伍排尾还是从从队伍排尾跑步到队伍排头,相对位移都是队伍的长度,当通讯员与队伍的运动方向相同时相对速度是两者速度的差,当通讯员与队伍的运动方向相反时相对速度是两者速度的和.

练习册系列答案
相关题目
14.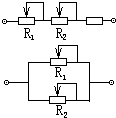 在电子仪器中.常用两个阻值不同的电位器(可变电阻)调节电路中的电流,一个做粗调(电流改变量大)一个做细调(电流改变量小)现连成如图所示两种方式已知R1>R2,则( )
在电子仪器中.常用两个阻值不同的电位器(可变电阻)调节电路中的电流,一个做粗调(电流改变量大)一个做细调(电流改变量小)现连成如图所示两种方式已知R1>R2,则( )
 在电子仪器中.常用两个阻值不同的电位器(可变电阻)调节电路中的电流,一个做粗调(电流改变量大)一个做细调(电流改变量小)现连成如图所示两种方式已知R1>R2,则( )
在电子仪器中.常用两个阻值不同的电位器(可变电阻)调节电路中的电流,一个做粗调(电流改变量大)一个做细调(电流改变量小)现连成如图所示两种方式已知R1>R2,则( )| A. | 串联时,R1做粗调 | B. | 串联时,R1做细调 | C. | 并联时,R1做粗调 | D. | 并联时,R1做细调 |
11.为提高百米赛跑运动员的成绩,教练员分析了运动员跑百米全程的录像带,测得:运动员在前7s跑了61m,7s末到7.1s末跑了0.92m,跑到终点共用10.8s,则下列说法不正确的是( )
| A. | 运动员在百米全过程的平均速度大小是9.26 m/s | |
| B. | 运动员在前7 s的平均速度大小是8.71 m/s | |
| C. | 运动员在7 s末的瞬时速度大小约为9.2 m/s | |
| D. | 无法估算运动员在7 s末的瞬时速度大小 |
18.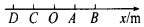 某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,0点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,0点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
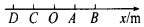 某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,0点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,0点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )| A. | 质点在A→B→C的时间内发生的位移为2 m,路程为4 m | |
| B. | 质点在B→D的时间内发生的位移为-4 m,路程为4 m | |
| C. | 当质点到达D点时,其位置可用D点的坐标-2 m表示 | |
| D. | 当质点到达D点时,相对于A点的位移为-5m |
8. 如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )
如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )
 如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )
如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )| A. | 此时小球的加速度大小为30m/s2 | |
| B. | 小球到达最高点时杆的弹力沿斜面向上 | |
| C. | 若增大v0,到达最高点时杆子对小球的弹力一定增大 | |
| D. | 若增大v0,到达最高点时杆子对小球的弹力可能减小 |
15.有四个运动的物体A、B、C、D,物体A、B运动的x-t图象如图①所示;物体C、D从同一地点沿同一方向运动的v-t图象如图②所示.根据图象做出的以下判断中正确的是( ) 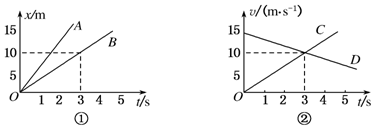
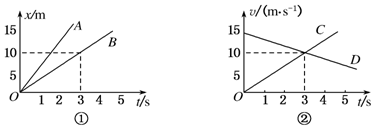
| A. | 物体A和B均做匀速直线运动,且A的速度比B更大 | |
| B. | 在0~3 s的时间内,物体B运动的位移为10 m | |
| C. | t=3 s时,物体C追上物体D | |
| D. | t=3 s时,物体C与物体D之间有最大间距 |
12.质量为m1=2kg,m2=5kg的两静止小车压缩一条轻弹簧后放在光滑的水平面上,放手后把小车弹开.今测得m2受到的冲量是10N•s,则在此过程中,m1的动量的变化量是( )
| A. | 2 kg•m/s | B. | -2 kg•m/s | C. | 10 kg•m/s | D. | -10 kg•m/s |
5. 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )| A. | 轻绳的长度为$\frac{2a}{b}$ | B. | 小球所带电荷量为$\frac{b+mg}{E}$ | ||
| C. | 小球在最高点的最小速度为$\sqrt{\frac{2a}{m}}$ | D. | 小球在最高点的最小速度为$\sqrt{\frac{5a}{m}}$ |