题目内容
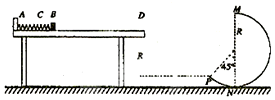
8. 如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )
如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )| A. | 此时小球的加速度大小为30m/s2 | |
| B. | 小球到达最高点时杆的弹力沿斜面向上 | |
| C. | 若增大v0,到达最高点时杆子对小球的弹力一定增大 | |
| D. | 若增大v0,到达最高点时杆子对小球的弹力可能减小 |
分析 先对小球受力分析,受细杆拉力、斜面弹力、重力,小球在出发点时,由细杆的拉力提供向心力,由圆周运动规律可列此时的表达式;
小球从释放到最高点的过程,在依据动能定理可知,速度越来越大,到达最高点时,轻杆对小球的弹力与小球的重力沿斜面的分力的合力提供向心力.
解答 解:A、小球做变速圆周运动,在初位置加速度不指向圆心,将其分解:
切向加速度为:$a′=\frac{mgsinα}{m}=gsinα$;
向心加速度为:${a}_{n}=\frac{{v}_{1}^{2}}{l}=\frac{{3}^{2}}{0.30}=30m/{s}^{2}$;
故时小球的加速度为合加速度,a=$\sqrt{{a}_{n}^{2}+a{′}^{2}}$>an=30m/s2>$\sqrt{30}$m/s2,故A错误;
B、从开始到最高点过程,根据动能定理,有:-mglsinα=$\frac{1}{2}{mv}_{1}^{2}-\frac{1}{2}{mv}_{0}^{2}$;
解得:v1=$\sqrt{{v}_{0}^{2}-2glsinα}$;
考虑临界情况,如果没有杆的弹力,重力的平行斜面分力提供向心力,有:$mgsinα=m\frac{{v}_{2}^{2}}{l}$,可以得到v2小于v1,说明杆在最高点对球是拉力,故B错误;
CD、在最高点时,轻杆对小球的弹力是拉力,故:$F+mgsinα=\frac{{mv}_{最高}^{2}}{l}$,如果初速度增大,则最高点速度也增加,故拉力F一定增加,故C正确,D错误;
故选:C.
点评 本题重点是分析小球圆周运动的向心力来源,这个情形虽然不是在竖直平面内的圆周运动,但是其原理和竖直平面内的圆周运动一样,要利用运动的合成与分解的观点结合牛顿第二定律求解.

 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案| A. | 小球的加速度方向不变,大小先减小后增大 | |
| B. | 小球的加速度方向不变,大小一直在减小 | |
| C. | 上升经历的时间一定小于下降经历的时间 | |
| D. | 上升到最高点时,小球的速度为零,加速度也为零 |
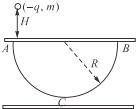 如图所示,平行板电容器的两个极板水平,两板之间固定一个光滑绝缘的半圆形轨道ACB,A、B为半圆轨道的两个端点,且A、B紧靠电容器的上极板,在A端对应位置的极板处开有一个小孔,C是轨道的最低点,半圆轨道半径为R.现使电容器的两板分别带等量异种电荷,使两板之间存在竖直向下的匀强电场,将一个质量为m、电荷量为-q的带电小球,从A点正上方高为H处由静止释放,小球由小孔进入电容器内部并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,下列说法中正确的是( )
如图所示,平行板电容器的两个极板水平,两板之间固定一个光滑绝缘的半圆形轨道ACB,A、B为半圆轨道的两个端点,且A、B紧靠电容器的上极板,在A端对应位置的极板处开有一个小孔,C是轨道的最低点,半圆轨道半径为R.现使电容器的两板分别带等量异种电荷,使两板之间存在竖直向下的匀强电场,将一个质量为m、电荷量为-q的带电小球,从A点正上方高为H处由静止释放,小球由小孔进入电容器内部并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,下列说法中正确的是( )| A. | 当匀强电场的电场强度大小E=$\frac{mg}{q}$时,带电小球在半圆形轨道内做匀速圆周运动 | |
| B. | 当匀强电场的电场强度大小E≤$\frac{mg(H+R)}{qR}$时,带电小球能沿轨道到达最低点 | |
| C. | 当匀强电场的电场强度大小E≤$\frac{mg(H+R)}{3qR}$时,带电小球能沿轨道到达最低点 | |
| D. | 将电容器的下极板向下移动一小段距离,则带电小球到达最低点C时的速率增大 |
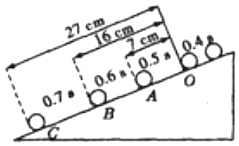 让小球从斜面的顶端滚下(如图所示标出了不同时刻小球沿斜面滚下的位置),试粗略计算:
让小球从斜面的顶端滚下(如图所示标出了不同时刻小球沿斜面滚下的位置),试粗略计算: